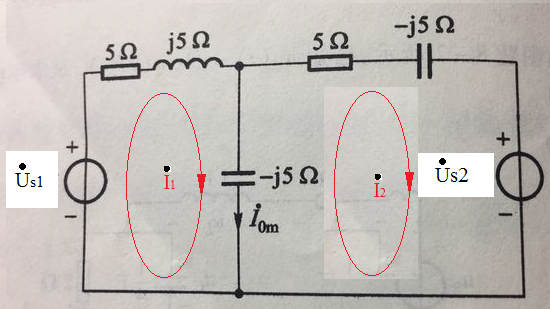
电路的相量模型怎么算电路的相量模型如图所示，试分别用网孔分析和节点

藏于心2023-03-21 06:43:012948

电路的相量模型如图所示，试分别用网孔分析和节点分析求解Iom(各电源电压相量均系振幅相量，电路的相量模型如图所示，试分别用网孔分析和节点，电路分析时相量计算怎么手算啊，就像2∠45+1∠？电路分析时相量计算怎么手算啊，就像2∠45+1∠？关于电路相量计算的问题，相量法的运算。

本文导航

电路的相量模型如图所示，试分别用网孔分析和节点分析求解Iom(各电源电压相量均系振幅相量)
电路的相量模型如图所示，试分别用网孔分析和节点
电路分析时相量计算怎么手算啊，就像2∠45+1∠
电路分析时相量计算怎么手算啊，就像2∠45+1∠
关于电路相量计算的问题？
相量法的运算

电路的相量模型如图所示，试分别用网孔分析和节点分析求解Iom(各电源电压相量均系振幅相量)

电路计算一般采用有效值相量，所以首先将电压源电压转化为有效值相量。

Us1（相量）=100/√2∠0°=50√2∠0° V；Us2（相量）=100/√2∠53.1°=50√2∠53.1° V。

1、网孔分析法，设定网孔电流如下图：

网孔1：（5+j5-j5）×I1（相量）-（-j5）×I2（相量）=Us1（相量）=50√2∠0°；

网孔2：（5-j5-j5）×I2（相量）+Us2（相量）-（-j5）×I1（相量）=0。

整理求解：I1（相量）=√2（4-j3）A，I2=√2×（3-j6） A。

所以：I0（相量）=I1（相量）-I2（相量）=√2（4-j3-3+j6）=√2（1+j3）A。

因此：I0m（相量）=√2×I0（相量）=√2×√2×（1+j3）=2+j6（A）。

2、节点电压法：设电容下端为公共节点O，上端的电位为U（相量）。

根据KCL：[U（相量）-Us1（相量）]/（5+j5）+U（相量）/（-j5）+[U（相量）-Us2（相量）]/（5-j5）=0。

解得：U（相量）=√2（15-j5）（V）。

因此：I0（相量）=U（相量）/（-j5）=√2（15-j5）/（-j5）=√2（1+j3）（A）。

所以：I0m（相量）=√2×I0（相量）=√2×√2×（1+j3）=2+j6（A）。

——本题也可以不将两个电压源的电压相量化为有效值相量，即直接采用振幅相量进行计算，因为所求的电容电流相量也是振幅相量，结果不变。

电路的相量模型如图所示，试分别用网孔分析和节点

电路计算一般采用有效值相量，所以首先将电压源电压转化为有效值相量。 Us1（相量）=100/√2∠0°=50√2∠0° V；Us2（相量）=100/√2∠531°=50√2∠531° V。 1、网孔分析法，设定网孔电流如下图：网孔1：（5+j5-j5）×I1（相量）-（-j5）×I2（相量）=Us电路的相量模型如图所示，试分别用网孔分析和节点

电路分析时相量计算怎么手算啊，就像2∠45+1∠

相量有两种表示形式：1、模+幅角；2、复数形式。

加减法时，采用复数形式计算。如果是“模+幅角”的形式，就转化为复数形式。如你的题目中：2∠45°+1∠30°=2×（cos45°+jsin45°）+1×（cos30°+jsin30°）=√2/2+j√2/2+√3/2+j0.5=（√2/2+√3/2）+j（0.5+√2/2）。

乘除法时：使用模+幅角形式计算。Z1=R1∠φ1，Z2=∠φ2，则：Z=Z1×Z2=R1∠φ1×R2∠φ2=R1R2∠（φ1+φ2）。如果是复数形式，就需要将其转化为模+幅角的形式：因为Z1=R1∠φ1=R1cosφ1+jR1sinφ1=x+jy，所以R1=√（x²+y²），φ1=arctan（y/x）。

此外，

复数阻抗的实部称为等效电阻，虚部称为电抗，模称为阻抗模，幅角称为阻抗角,它们分别用符号R、X、|Z|、φ表示。复数导纳的实部称为等效电导，虚部称为电纳，模称为导纳模，幅角称为导纳角，它们分别用符号G、B、|Y|、φ┡表示，于是 Z =R+jX=|Z|e。

扩展资料：

例1：电路分析时相量计算，2∠45+1∠-30 计算：

加减用代数式,乘除用指数式,本题是加减,要转换成代数式：

2∠45 + 1∠-30

= 2 cos45° + j 2 sin45° + cos(- 30°) + j sin(- 30°)

= √2 + j √2 + √3/2 - j 0.5

= (√2 + √3/2) + j (√2 - 0.5)

= 2.28 + j0.9142

= 2.456∠21.84°

例2：电路分析时相量计算，2∠45：

相量有两种表示形式：1、模+幅角；2、复数形式。加减法时，采用复数形式计算。如果是“模+幅角”的形式，就转化为复数形式。如你的题目中：2∠45°+1∠30°=2×（cos45°+jsin45°）+1×（cos30°+jsin30°）=√2/2+j√2/2+√3/2+j0.5=（√2/2+√3/2）+j（0.5+√2）。

参考资料：百度百科 --- 相量

电路分析时相量计算怎么手算啊，就像2∠45+1∠

相量加减分析要用平行四边形法则，特殊角度好算，非特殊角度可以化成复数后再运算。

相量乘除法运算较简单，乘法：模相乘、角度相加，出发模相处，角度相减。

如果幅角都是特殊角度的话，还能进行纯手工计算;

如：2∠45°+2∠60°=2×（√2/2+j√2/2）+2×（1/2+j√3/2）=√2+j√2+1+j√3=（1+√2）+j（√2+√3）=......

但是如果不是特殊角度，如果非要采用手工计算，恐怕就得使用三角函数表了（也就是中学常用的《学生数学用表》）。否则一般角度的正余弦值是得不出来的，要不然就得使用计算器。

扩展资料：

相量仅适用于频率相同的正弦电路.由于频率一定,在描述电路物理量时就可以只需考虑振幅与相位,振幅与相位用一个复数表示,其中复数的模表示有效值,辐角表示初相位.这个复数在电子电工学中称为相量。

两同频率正弦量叠加,表述为:Asin(ωt+α)+Bsin(ωt+β)=(Acosα+Bcosβ)sinωt+(Asinα+Bsinβ)cosωt.易知,叠加后频率没变,相位变化,而且服从相量(复数)运算法则.故相量相加可以描述同频率正弦量的叠加。

相量的的乘除可以表示相位的变化,例如:电感Ι电压超前电流90度,用相量法表示为U=jχI,其中j为单位复数,χ为感抗。

参考资料来源：搜狗百科-相量

关于电路相量计算的问题？

问题点比较多，一个个来回答。

1、相量计算乘、除时，乘法角度相加，除法角度相减，这是没错的；

2、U（相量）=380∠-53.1°V，I（相量）=10∠30°A，则：φu=-53.1°，φi=30°，φ=φu-φi=-53.1°-30°=-83.1°。有功功率：P=UIcosφ=380×10×cos（-83.1°）。你的表达式为：10×380∠83.1°是错误的，因为这个式子还是个相量，这个式子继续展开为：380×10×（cos83.1°+jsin83.1°），是个复数，而有功功率不可能是相量（复数）。所以有功功率的求法是：电压有效值×电流有效值×cosφ，其中φ为电压相位（φu）与电流相位（φi）的相位差，而不是你以为的式子。你的式子是错误的。

3、电路的功率也可以用复功率来表达：S*=U（相量）×I*，其中S*表示复功率，S*=P+jQ；I*表示电流相量I（相量）的共轭复数。，例如：I（相量）=10∠30°=10（√3/2+j1/2）=5√3+j5（A），那么：I*=5√3-j5=10∠-30°；I*只是一个复数而不是相量。

这样：S*=380∠-53.1°×10∠-30°=380×10∠-83.1°=3800×（cos83.1°-jsin83.1°）=P+jQ。

P=3800cos83.1°（W），Q=-3800sin83.1°（var），其中Q的负值代表电路呈现容性，向外部提供无功功率。