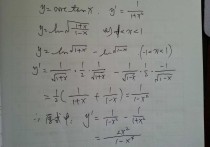函数定理3怎么证明 高等数学:如图,定理3的这三个命题用函数极限的定义证明怎么证明?帮我写出证明过程,谢谢!
三次函数韦达定理如何推导?隐函数存在定理3怎么推导的?高数上37页 函数的极限 定理3的推论的 证明,高等数学同济第七版函数极限的性质定理3怎么证明(⊙_⊙??高等数学:如图,定理3的这三个命题用函数极限的定义证明怎么证明?帮我写出证明过程,谢谢?函数有界性的定理如何证明?
本文导航
- 三次函数韦达定理如何推导
- 隐函数存在定理3怎么推导的?
- 高数上37页 函数的极限 定理3的推论的 证明
- 高等数学同济第七版函数极限的性质定理3怎么证明(⊙_⊙?)
- 高等数学:如图,定理3的这三个命题用函数极限的定义证明怎么证明?帮我写出证明过程,谢谢!
- 函数有界性的定理如何证明
三次函数韦达定理如何推导
众所周知,对于一元二次方程ax^2+bx+c=0,(a≠0)
两根x1,x2
有如下关系
x1+x2=-b/a
x1x2=c/a
|x1-x2|=√△/|a|
对于第三个,证法很简单了,就是依靠1式平方与二式乘4做差开根号。
前两个,
一是用求根公式,x=(-b±√△)/2a
加起来、乘起来,即可得到
x1+x2=-b/a
x1x2=c/a
的关系
这种证法的优点是,第三个式子用这个方法也可以很轻松证明出来
二是用分解式,若有两根x1,x2,则原方程显然可以化成
a(x-x1)(x-x2)=0
展开可得ax^2-a(x1+x2)x+ax1x2=0
对应上面的ax^2+bx+c=0
亦可得
x1+x2=-b/a
x1x2=c/a
的关系
这种证法的优点,下面会叙述。
韦达定理除了不解方程知道方程根的关系外,还可以用来构造方程
如:x^2-3x+1=0
两根x1+x2=3/2
x1x2=1
但是不用韦达定理的话就很悲催了。要出人命的。
又如
已知a+b=2,ab=1
求a,b
利用韦达定理,以a,b,为两根的方程x^2-(a+b)x+ab=0
即x^2-2x+1=0
a=b=1
但是利用韦达定理需要许多限制。
如:求x^2-3x+5=0根的关系
有人直接写,x1x2=5,x1+x2=3/2
但是注意:△=3^2-4*5=9-20=-11<0
方程根本没有根!
所以说,用韦达定理,必须先检验:(1)二次项系数不为0,(2)△≥0
下面叙述分解式求证韦达定理的优点。
对于三次方程ax^3+bx^2+cx+d=0
当然你是可以用求根公式来做,但三次方程的求根公式,。。。无法想象。
所以,设三根为x1,x2,x3
则原方程化为a(x-x1)(x-x2)(x-x3)=0
展开
ax^3-a(x1+x2+x3)x^2+a(x1*x2+x2*x3+x3*x1)-ax1*x2*x3=0
x1+x2+x3=-b/a
x1*x2+x2*x3+x3*x1=c/a
x1*x2*x3=-d/a
同理,四次方程也可以如是解决。(当然是比较可怕的,但是绝对可以搞定)
隐函数存在定理3怎么推导的?
首先,该定理先证明了u和v在局部上是x的函数,并且可导。
由于u(x), v(x)对x,可导,在
F(u, v, x) = 0, G(u, v, x) = 0中分别对x求导(用链式法则),就得到了上面的方程组
此线性方程组在每一个特定的点处成立,把它看作关于变量“偏u/偏x”, “偏v/偏x”的线性方程组,其它项视作常数(注意这个方程组的意义在于它在每一点处成立,在任一个点处当然是常数)用线性代数中的Grammer法则即可。(上述出现的行列式就是Grammer法则中的行列式。)
高数上37页 函数的极限 定理3的推论的 证明
取ε=|A|&#47;2,用极限定义对ε=|A|&#47;2存在正数δ,当0<|x-x0|<δ时,有|f(x)-A|<ε=|A|&#47;2,所以|f(x)|=|f(x)-A+A|≥|A|-|f(x)-A|>|A|&#47;2
高等数学同济第七版函数极限的性质定理3怎么证明(⊙_⊙?)
高等数学:如图,定理3的这三个命题用函数极限的定义证明怎么证明?帮我写出证明过程,谢谢!
limf=A,limg=B,则:
对0<|x-x0|<δ1,|f-A|<ε1
对0<|x-x0|<δ2,|g-B|<ε2
取δ=min[δ1,δ2],则当0<|x-x0|<δ时,|f-A|<ε1和|g-B|<ε2都成立
∴|f+g-A-B|≤|f-A|+|g-B|<ε1+ε2=ε
即证明了lim(f+g)=A+B
其他同理
函数有界性的定理如何证明
需使用3个定理如下:
定理1:任意数列{Ut}满足:m≤Ut≤n,
则有{Ut}的子列{U(t(s))}收敛。
定理2:[m,n]中的所有有理数可记为
数列{Rt}。
定理3:[m,n]中的所有数x,
有[m,n]中有理数列{At},使
x=Lim{t→∞}At=x
1。设函数f于区间[m,n]内有连续
设[m,n]中的所有有理数数列{Rt}(定理2),
定义数列{Pt},使Pt=Rs,
满足:f(Pt)=Max{f(Rs),1≤s≤t}
由定理1得:有{Pt}的子列{Pt(s)}收敛,
设Lim{s→∞}Pt(s)=y。
2。任意:[m,n]中的数x,定理3得:
有[m,n]中有理数列{At},使
x=Lim{t→∞}At=x。
ⅰ。对于任意ε>0,由f在x的连续性得:有
f(At)>f(x)-ε
ⅱ。由f在y的连续性得:有S,当s≥S
f(y)>f(Pt(s))-ε
ⅲ。At是[m,n]中的有理数,则
At=Ru,取v≥S,使
t(v)≥u,则有
f(Pt(v))=Max{f(Rs),1≤s≤t}
≥f(Ru)=f(At)
==》f(y)+ε>f(Pt(v))≥f(At)>f(x)-ε
==》f(y)≥f(x)==》
f(y)最大值。
3。同理f最小值.