怎么看数列收敛还是分散 如何判断数列收敛还是发散？

怎样判别一个数列是发散还是收敛？如何判断数列收敛或发散？怎么判断函数和数列是收敛或发散的？如何判断一个数列是发散还是收敛？如何判断数列收敛还是发散？如何判断一个数列是发散还是收敛？

本文导航

• 怎样判别一个数列是发散还是收敛？
• 如何判断数列收敛或发散？
• 怎么判断函数和数列是收敛或发散的
• 如何判断一个数列是发散还是收敛？
• 如何判断数列收敛还是发散？
• 如何判断一个数列是发散还是收敛

怎样判别一个数列是发散还是收敛？

加减的时候， 把高阶的无穷小直接舍去

如 1 + 1/n, 用1来代替

乘除的时候， 用比较简单的等价无穷小来代替原来复杂的无穷小来

如 1/n * sin(1/n) 用1/n^2 来代替

如果数列项数n趋于无穷时，数列的极限==实数a，那么这个数列就是收敛的；如果找不到实数a，这个数列就是发散的。

如何判断数列收敛或发散？

看n趋向无穷大时,Xn是否趋向一个常数,可是有时Xn比较复杂,并不好观察,

加减的时候,把高阶的无穷小直接舍去

如 1 + 1/n,用1来代替

乘除的时候,用比较简单的等价无穷小来代替原来复杂的无穷小来

如 1/n * sin(1/n) 用1/n^2 来代替

怎么判断函数和数列是收敛或发散的

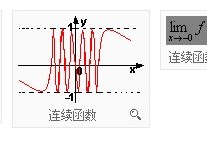
收敛函数：若函数在定义域的每一点都收敛,则通常称函数是收敛的。函数在某点收敛,是指当自变量趋向这一点时，其函数值的极限就等于函数在该点的值。有界函数指的是对于定义域中的任意一个值,相应的函数值都在一个区间内变化，也就是函数值的绝对值总小于某一个固定值，那函数就是有界的。

收敛函数一定有界，但是有界函数不一定收敛，如f(x)在x=0处f(0)=2，在其他x处f(x)=1，那么f(x)在x=0处就不是收敛的，那么f(x)就不是收敛函数，但是f(x)是有界的,因为1≤f(x)≤2。

判断数列是否收敛或者发散：

1、设数列{Xn}，如果存在常数a，对于任意给定的正数q（无论多小），总存在正整数N，使得n>N时，恒有|Xn-a|<q成立，就称数列{Xn}收敛于a（极限为a），即数列{Xn}为收敛。

2、求数列的极限，如果数列项数n趋于无穷时，数列的极限能一直趋近于实数a，那么这个数列就是收敛的；如果找不到实数a，这个数列就是发散的。看n趋向无穷大时,Xn是否趋向一个常数,可是有时Xn比较复杂,并不好观察。这种是最常用的判别法是单调有界既收敛。

3、加减的时候,把高阶的无穷小直接舍去如 1 + 1/n,用1来代替乘除的时候,用比较简单的等价无穷小来代替原来复杂的无穷小来如 1/n * sin(1/n) 用1/n^2 来代替

4、收敛数列的极限是唯一的，且该数列一定有界，还有保号性，与子数列的关系一致。不符合以上任何一个条件的数列是发散数列。另外还有达朗贝尔收敛准则,柯西收敛准则,根式判敛法等判断收敛性。

拓展资料：

函数极限是高等数学最基本的概念之一，导数等概念都是在函数极限的定义上完成的。

函数极限可以分成x→∞,x→+∞,x→-∞,x→Xo,，而运用ε-δ定义更多的见诸于已知极限值的函数极限证明题中。掌握这类证明对初学者深刻理解运用极限定义大有裨益。

以x→Xo 的极限为例，f(x) 在点Xo 以A为极限的定义是： 对于任意给定的正数ε（无论它多么小），总存在正数δ ，使得当x满足不等式0<|x-x。|<δ 时，对应的函数值f(x)都满足不等式： |f(x)-A|<ε ，那么常数A就叫做函数f(x)当 x→x。时的极限。

问题的关键在于找到符合定义要求的 ，在这一过程中会用到一些不等式技巧，例如放缩法等。1999年的研究生考试试题中，更是直接考察了考生对定义的掌握情况。

如何判断一个数列是发散还是收敛？

看n趋向无穷大时，Xn是否趋向一个常数，即可以判断收敛还是发散。

可是有时Xn比较复杂，并不好观察,加减的时候，把高阶的无穷小直接舍去如 1 + 1/n，用1来代替乘除的时候，用比较简单的等价无穷小来代替原来复杂的无穷小。

收敛函数一定有界，但是有界函数不一定收敛，如f(x)在x=0处f(0)=2，在其他x处f(x)=1，那么f(x)在x=0处就不是收敛的，那么f(x)就不是收敛函数，但是f(x)是有界的,因为1≤f(x)≤2。

基本公式：

1、一般数列的通项an与前n项和Sn的关系：an=Sn-Sn-1。

2、等差数列的通项公式：an=a1+(n-1)d; ; ; an=ak+(n-k)d; ; ;(其中a1为首项、ak为已知的第k项); 当d≠0时，an是关于n的一次式；当d=0时，an是一个常数。

3、等差数列的前n项和公式：Sn=An^2+Bn; ; ;Sn=na1+[n(n-1)]d/2; ;Sn=(a1+an)n/2。

当d≠0时，Sn是关于n的二次式且常数项为0；当d=0时（a1≠0），Sn=na1是关于n的正比例式。

4、等比数列的通项公式： an= a1 qn-1; ; an= ak qn-k; (其中a1为首项、ak为已知的第k项，an≠0)。

5、等比数列的前n项和公式：当q=1时，Sn=n a1; ; ;(是关于n的正比例式)。

如何判断数列收敛还是发散？

看n趋向无穷大时，Xn是否趋向一个常数，即可以判断收敛还是发散。

可是有时Xn比较复杂，并不好观察,加减的时候，把高阶的无穷小直接舍去如 1 + 1/n，用1来代替乘除的时候，用比较简单的等价无穷小来代替原来复杂的无穷小。

收敛函数一定有界，但是有界函数不一定收敛，如f(x)在x=0处f(0)=2，在其他x处f(x)=1，那么f(x)在x=0处就不是收敛的，那么f(x)就不是收敛函数，但是f(x)是有界的,因为1≤f(x)≤2。

扩展资料：

日常生活中，人们常常用到等差数列如：在给各种产品的尺寸划分级别时，当其中的最大尺寸与最小尺寸相差不大时，常按等差数列进行分级。若为等差数列，且有an=m，am=n，则am+n=0。其于数学的中的应用，可举例：

快速算出从23到132之间6的整倍数有多少个，算法不止一种，这里介绍用数列算令等差数列首项a1=24（24为6的4倍），等差d=6；于是令an= 24+6(n-1)<=132 即可解出n=19。

如何判断一个数列是发散还是收敛

方法/步骤：