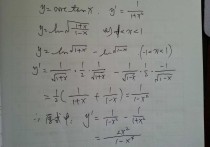怎么判断分段函数的可导性 分段函数可导一定连续是正确的吗
怎么在确定一个函数在一段区间的可导性?高等数学太有意思了怎样判断一个分段函数是否有导数?分段函数可导性判断,分段函数在某点的可导性,分段函数的可导性,如何证明分段函数在某点处的连续性和可导性?
本文导航
怎么在确定一个函数在一段区间的可导性
1、如果是初等函数,则在定义域上用复合函数求导,可直接求导,则导数存在;对于复合函数求导表达式中,如果出现有分母,则分母为0的点,应用导数定义判断是否可导。
2、如果分段函数,则分界点处是否可导,应用导数定义判断是否可导
高等数学太有意思了怎样判断一个分段函数是否有导数
函数可导,那么此函数必定连续,而函数连续却未必可导!对于分段函数来说,你需要用导数的定义去求它的导数,特别是分段点的导数!你需要求出它在分段点的左,右导数,看是否相等来进行判断!说白了,导数的物理意义其实就是变化率的问题,它体现的是一种连续变化的观念!比如说,位移对时间的导数体现的就是速度,速度对时间的导数,体现的就是加速度等等!!
分段函数可导性判断
e^n(x-1)是趋于无穷
函数在某点连续与可导的关系
首先看函数在该点是否连续,如果不连续则肯定不可导,如果连续再进行下一步:看函数的左导数是否等于右导数,如果左右导数均存在且相等,这个判断分段函数在该点可导。
分段函数可导一定连续是正确的吗
第一个:左右导数既然都存在利用定义可以证明左右极限相等所以连续。第二个:你要明白不管左导还是右导定义中f(x0),也就是你题目中的f(0)只有一个就是1,你第二个式子明显把0带入x-1了,题目规定有f(0)=x+1=1不会变
如何证明分段函数在某点处的连续性和可导性
分段函数在分段点上的可导性的证明,需要用左右导数的定义去求其左右导数是否存在并且相等.
比如你的例子里
f(x)在0处的左导数是1,右导数也是1,所以,函数在该点是可导的