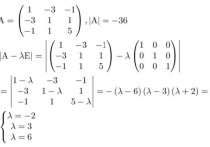什么矩阵的秩等于1 怎么看出矩阵的秩是1
秩为1矩阵?有什么性质?矩阵的秩在什么情况下=0,1?矩阵的秩在什么情况下=0、1、n?为什么矩阵的秩为一有这个结果?单位矩阵的秩是什么?对称矩阵的秩为什么为1?
本文导航
为什么单位矩阵的秩等于1
设A是秩为1的n阶方阵, 则
1. A可表示为αβ^T, 其中α,β为n维列向量
2. A^k = (α^Tβ)^(k-1)A
3. tr(A)=α^Tβ
4. A的特征值为 α^Tβ,0,0,...,0
注: α^Tβ=β^Tα
矩阵的秩与零行个数的关系
矩阵的秩等于0的充分必要条件是这个矩阵是零矩阵。矩阵的秩等于1的充分必要条件是这个矩阵非零且各行各列都成比例。
通俗易懂理解矩阵的秩
当矩阵为0矩阵时
秩=0,当矩阵内行向量不含0向量,且线性相关时秩=1,矩阵可逆时秩=n
为什么矩阵内积的秩等于矩阵的秩
因为由矩阵的初等行变换,第二行减去第一行的三倍,即r2-3r1,第二行全部变为零,只剩第一行为非零行,因此矩阵的秩为1。也可以这样理解,这个二阶方阵的任何一个一阶子式都非零,而二阶行列式为零,因此矩阵的秩为1。
矩阵的秩怎么查
单位矩阵的秩是1。
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
根据单位矩阵的特点,任何矩阵与单位矩阵相乘都等于本身,而且单位矩阵因此独特性在高等数学中也有广泛应用。单位矩阵的特征值皆为1,任何向量都是单位矩阵的特征向量。因为特征值之积等于行列式,所以单位矩阵的行列式为1。
矩阵的秩:
定理:矩阵的行秩,列秩,秩都相等。
定理:初等变换不改变矩阵的秩。
定理:如果A可逆,则r(AB)=r(B),r(BA)=r(B)。
定理:矩阵的乘积的秩Rab<=min{Ra,Rb};
引理:设矩阵A=(aij)sxn的列秩等于A的列数n,则A的列秩,秩都等于n。
当r(A)<=n-2时,最高阶非零子式的阶数<=n-2,任何n-1阶子式均为零,而伴随阵中的各元素就是n-1阶子式再加上个正负号,所以伴随阵为0矩阵。
当r(A)<=n-1时,最高阶非零子式的阶数<=n-1,所以n-1阶子式有可能不为零,所以伴随阵有可能非零(等号成立时伴随阵必为非零)。
怎么看出矩阵的秩是1
对称矩阵的秩为1是因为A的所有特征值的和是1。在数学中,矩阵是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。