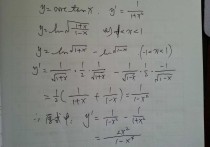极坐标交换积分次序怎么看 二重积分极坐标变化,交换积分顺序上下极限怎么确定
极坐标下交换积分次序如何求解呀? 有图最好,帮忙解释一下?在极坐标下交换积分次序的一道题,极坐标下交换积分次序怎么求解呀?【高数】交换积分(极坐标)的次序,二重积分极坐标变化,交换积分顺序上下极限怎么确定?极坐标下,二重积分如何变换积分次序……我到现在都没搞懂,求学霸详解,要有例题,谢谢?
本文导航
极坐标求二重积分的步骤
1、本题的积分区域,请参看下面的第一张图片;
2、原来的积分次序,一次性地包括了粉红色部分跟草绿色部分;
3、交换积分次序后,积分区域就变成了两部分 : 粉红色部分 + 草绿色部分;
4、极坐标积分的积分次序的意思是:
A、先对 r 积分的意思
---一个极经,从原点射出 r = 0,射到极坐标方程的曲线上;
---然后这个极经,逆时针扫过的角度,就是θ的范围。
B、先对;θ 积分的思想
---从圆心开始画同心圆弧,圆弧的角度,也就是圆心角 central angle,
; ;逆时针从最下方的曲线或直线上的角度,扫到最上方的曲线或直线上的角度,
; ;这个角度必要用极坐标方程表示,也就是必须是 r 的函数;
---然后从扫过的范围中,确定 r 是从多少到多少,都是具体的数字。
有了这些思想,就容易看懂第二张图片的解答了。
如有疑问,欢迎追问,有问必答、有疑必释,有错必纠。
在极坐标下交换积分次序的一道题。
1、本题的积分区域,请参看下面的第一张图片;
2、原来的积分次序,一次性地包括了粉红色部分跟草绿色部分;
3、交换积分次序后,积分区域就变成了两部分 : 粉红色部分 + 草绿色部分;
4、极坐标积分的积分次序的意思是:
A、先对 r 积分的意思
---一个极经,从原点射出 r = 0,射到极坐标方程的曲线上;
---然后这个极经,逆时针扫过的角度,就是θ的范围。
B、先对;θ 积分的思想
---从圆心开始画同心圆弧,圆弧的角度,也就是圆心角 central angle,
逆时针从最下方的曲线或直线上的角度,扫到最上方的曲线或直线上的角度,
这个角度必要用极坐标方程表示,也就是必须是 r 的函数;
---然后从扫过的范围中,确定 r 是从多少到多少,都是具体的数字。
有了这些思想,就容易看懂第二张图片的解答了。
极坐标下交换积分次序怎么求解呀
请仔细阅读,体会其中的解题思想:
【高数】交换积分(极坐标)的次序。
原积分可写为∫∫f(r,t)drdt
(以t代替角度)
=∫∫[f(r,t)/r]rdrdt可看成某二重积分
其积分区域为圆心为(a/2,0),半径为a/2的圆
交换积分顺序后,固定
r,原点为圆心r为半径的圆与上圆交点处的t值为arccos(r/a),-arccos(r/a)
r在(0,a)内两圆有交点
如2L所说
交换后t下限、上限分别为:-arccos(a/r)与arccos(a/r)
r从0到a
而r是否遗漏并不重要
因为f(r,t)=[f(r,t)/r]*r可提出r
二重积分极坐标变化,交换积分顺序上下极限怎么确定
交换顺序时,暂时忘掉极坐标的含义,把θ与r当作直角坐标就容易做。
c比如,区域为
x²+y²≤x
极坐标系下先ρ后θ的积分区域表示成
-π/2≤θ≤π/2
0≤ρ≤cosθ
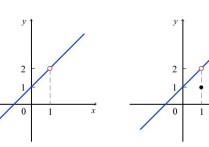
然后,建立以θ为横坐标,ρ为纵坐标的直角坐标系,
区域变成由
ρ=cosθ (-π/2≤θ≤π/2)和θ轴围成的区域,
改变积分次序后,变成
0≤ρ≤1
-arccosρ≤θ≤arccosρ
扩展资料:
极坐标是指在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向)。
对于平面内任何一点M,用ρ表示线段OM的长度(有时也用r表示),θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对 (ρ,θ)就叫点M的极坐标,这样建立的坐标系叫做极坐标系。通常情况下,M的极径坐标单位为1(长度单位),极角坐标单位为rad(或°)。
参考资料来源:百度百科-极坐标
用极坐标计算二重积分角度怎么算
一般场合,极坐标系下二重积分的计算,都是遵循先ρ后θ的形式,少数场合需要交换次序的时候,按下面步骤来:
(1)先按先ρ后θ的次序写好。
(2)再把关于ρ和θ的区域直接转换成直角坐标系。
按照直角坐标系下交换积分次序的方法完成。
比如,区域为x²+y²≤x;
极坐标系下先ρ后θ的积分区域表示成-π/2≤θ≤π/2;
0≤ρ≤cosθ;
然后,建立以θ为横坐标,ρ为纵坐标的直角坐标系,区域变成由ρ=cosθ (-π/2≤θ≤π/2)和θ轴围成的区域,改变积分次序后,变成0≤ρ≤1-arccosρ≤θ≤arccosρ这样就可以了。
二重积分:
二重积分是二元函数在空间上的积分,同定积分类似,是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用,可以用来计算曲面的面积,平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的(有向)曲面上进行积分,称为曲面积分。