数列极限怎么计算公式 数列极限的求法
怎么求数列的极限?数列极限的求法,求极限的四则运算公式,数列的极限怎么算?lim的基本计算公式。
本文导航
怎么求数列的极限?
求极限常见的方法:四则运算,连续,换元代换,等价代换.分母有理化.二个重要极限,二个重要法则.洛必达法则(对七种不定式),泰勒公式.级数方法.
后面二种方法用得比较少.前面的都是常用到的方法
四则运算方法:对有理分式x-->无穷时,一般是上下同除以分母的最高次幂.
x-->0时,一般是上下同除以分子的最高次幂.
对无理分式.一般是分子或分母有理化.
其它的有变量代换等.
最后一般都可以直接代入求了
数列极限的求法
数列极限的求法:
1、如果代入后,得到一个具体的数字,就是极限。
2、如果代入后,得到的是无穷大,答案就是极限不存在。
3、如果代入后,无法确定是具体数或是无穷大,就是不定式类型,
4、计算极限,就是计算趋势 tendency。
存在条件:
单调有界定理 在实数系中,单调有界数列必有极限。
致密性定理,任何有界数列必有收敛的子列。
计算方法,参考下面图片:
拓展资料数列的极限问题是我们学习的一个比较重要的部分,同时,极限的理论也是高等数学的基础之一。数列极限的问题作为微积分的基础概念,其建立与产生对微积分的理论有着重要的意义。
极限:
解题思路:
参考资料:百度百科-数列极限
常见的求极限公式大全
lim[f(x)±g(x)]=limf(x)±limg(x)这个公式有个前提
那就是limf(x)和limg(x)两个极限都必须存在,都必须是有限常数。极限∞(含±∞)是极限不存在的一种情况。
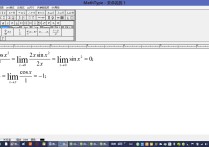
你的做法中,limx→∞x²和limx→∞
x两个极限都是∞,都不存在。
所以不满足公式应用的前提,这是公式套用错误。
类似的,极限乘除法,也都要求各个极限是存在的(不能为∞)。除法还要求分母的极限不能是0
数列的极限怎么算
求数列极限的步骤:认识数列极限的定义及性质,了解证明数列极限的基本方法,学习例题,看题干解问题,利用定义来证明数列的极限,检查解答过程。
求数列极限的步骤
1求数列极限的步骤
1.认识数列极限的定义及性质。即最终数列发展到第无限项的时候,数列的数值是归于一个固定数的。
2.了解证明数列极限的基本方法。主要是通过数列的子数列进行证明。
3.学习例题,看题干解问题。主要看数列的定义和相关关于数列的题设
4.利用定义来证明数列的极限。注意!只能利用定义来进行求取和证明,不可通过性质。
5.检查解答过程,发现解题过程中的问题进行修改。保证问题解决!
2数列极限定义
设{Xn}为实数列,a为定数.若对任给的正数ε,总存在正整数N,使得当n>N时有∣Xn-a∣<ε则称数列{Xn}收敛于a,定数a称为数列{Xn}的极限,并或Xn→a(n→∞)
读作"当n趋于无穷大时,{Xn}的极限等于或趋于a".
若数列{Xn}没有极限,则称{Xn}不收敛,或称{Xn}为发散数列.
该定义常称为数列极限的ε-N定义.
对于收敛数列有以下两个基本性质,即收敛数列的唯一性和有界性。
定理1:如果数列{Xn}收敛,则其极限是唯一的。
定理2:如果数列{Xn}收敛,则其一定是有界的。即对于一切n(n=1,2……),总可以找到一个正数M,使|Xn|≤M。
数列的极限问题是我们学习的一个比较重要的部分,同时,极限的理论也是高等数学的基础之一。数列极限的问题作为微积分的基础概念,其建立与产生对微积分的理论有着重要的意义。
唯一性 若数列 收敛,则它只有一个极限。
有界性 若数列 收敛,则 为有界数列,即存在正数 ,使得对一切正整数n有
保号性 若 (或 ),则对 (或 ),存在正数N,使得当 时,有 (或 )。
保不等式性 设 与 均为收敛数列。若存在正数 ,使得当 时有 ,则
迫敛性 设收敛数列 , 都以a为极限,数列 满足:
存在正数 ,当 时有 则数列 收敛,且
lim的基本计算公式
lim的基本计算公式:lim f(x) = A 或 f(x)->A(x->+∞)。
设 {Xn} 为实数列,a 为定数.若对任给的正数 ε,总存在正整数N,使得当 n>N 时有∣Xn-a∣<ε 则称数列{Xn};收敛于a,定数 a 称为数列 {Xn} 的极限,并记作,或Xn→a(n→∞)读作“当 n 趋于无穷大时,{Xn} 的极限等于 或 趋于 a”。
对于收敛数列有以下两个基本性质,即收敛数列的唯一性和有界性。如果数列{Xn}收敛,则其极限是唯一的。如果数列{Xn}收敛,则其一定是有界的。即对于一切n(n=1,2……),总可以找到一个正数M,使|Xn|≤M。
扩展资料:
与常数a的接近程度。ε越小,表示接近得越近;而正数ε可以任意地变小,说明xn与常数a可以接近到任何不断地靠近的程度。但是,尽管ε有其任意性,但一经给出,就被暂时地确定下来,以便靠它用函数规律来求出N;
又因为ε是任意小的正数,所以ε/2 、3ε 、ε等也都在任意小的正数范围,因此可用数值近似代替ε。同时,正由于ε是任意小的正数,可以限定ε小于一个某一个确定的正数。
参考资料来源:百度百科-lim