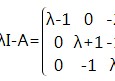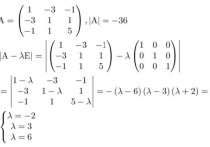什么叫秩为1的矩阵 矩阵的秩与特征值之间的关系
秩为1的矩阵长什么样,可否举一个简单的例子?秩为1矩阵?有什么性质?秩等于1的矩阵,它的特征值为什么是这样的?秩为1的矩阵性质总结是什么?秩为一的矩阵的特征值是什么?秩等于1的矩阵都有什么特征?
本文导航
矩阵的秩的本质是什么
矩阵秩为1,即极大线性无关组为1,比如以下矩阵:
矩阵的秩为1的例子
设A是秩为1的n阶方阵,则
1、A可表示为αβ^T,其中α,β为n维列向量。
2、A^k=(α^Tβ)^(k-1)A
3、tr(A)=α^Tβ
4、A的特征值为α^Tβ,0,0,...,0
注:α^Tβ=β^Tα
扩展资料
秩等于1的矩阵的定义:
秩等于1的矩阵是一类特殊的矩阵,它一定可以表示为一个非零列向量(列矩阵)与一个非零行向量(行矩阵)的乘积,根据矩阵乘法的结合律这类矩阵的乘法和方幂运算可以大大简化;这类矩阵的特征值与特征向量具有其特殊性。
如何判断矩阵的秩为1
秩小于行或者列的个数n,说明矩阵的行列式值等于0,而矩阵行列式等于特征值的乘积,所以一定会有零为特征值。
对于秩为1的n阶矩阵,零是其n重或n-1重特征值,如果是n-1重,则非零特征值是矩阵的主对角线元素之和;另外还看到,秩为1的矩阵可以分解为一个非零列向量与另一个非零列向量的转置的乘积,这两个向量的内积即是非零特征值;秩为1的矩阵对应的齐次线性方程组的基础解系含n-1个解向量。
秩等于1的方阵的对角化问题:
矩阵A可对角化的充分必要条件是:A有n个线性无关的特征向量。
对于秩等于1的n(n2)阶矩阵A=aT,a,均为n维非零列向量,齐次线性方程组AX=0的基础解系含有n-1个线性无关的解向量a2=(-b2,b1,0,..0)T,a3=()J3,D,),.....,an=-n,0,..,b1)T,它们是A对应于特征值入=0的n-1个线性无关的特征向量。
矩阵的秩的简单理解
性质总结如下:
1、对于秩为1的n阶矩阵,零是其n重或n-1重特征值,如果是n-1重,则非零特征值是矩阵的主对角线元素之和。
2、另外还看到,秩为1的矩阵可以分解为一个非零列向量与另一个非零列向量的转置的乘积,这两个向量的内积即是非零特征值;秩为1的矩阵对应的齐次线性方程组的基础解系含n-1个解向量。
秩1矩阵形如以下形式:
一、基本性质1、2、3的秩,则存在常数,使得,此时是秩1矩阵4,则存在。
二、特征值1的特征值为0(n-1重),(1重)。2的特征值为0(n重)。正定,是n维的非零实列向量,特征值为0(n-1重),(1重)。
三、对角化的最小多项式。当可对角化;当不可对角化,所以存在可逆矩阵,使得特别的实对称阵,则一定可对角化存在可逆矩阵。
矩阵的秩与特征值之间的关系
秩为1的矩阵,1个非零特征值是矩阵的迹, 即对角元元素之和, 其它特征值均为0。
对于秩为1的n阶矩阵,零是其n重或n-1重特征值,如果是n-1重,则非零特征值是矩阵的主对角线元素之和。
另外还看到,秩为1的矩阵可以分解为一个非零列向量与另一个非零列向量的转置的乘积,这两个向量的内积即是非零特征值,秩为1的矩阵对应的齐次线性方程组的基础解系含n-1个解向量。
定义:
由定义直接可得n阶可逆矩阵的,秩为n,通常又将可逆矩阵称为满秩矩阵, det(A)70,不满秩矩阵就是奇异矩阵,det(A)=0。矩阵A的转置AT的秩与A的秩是一样的,即rank(A)=rank(AT)。
当r(A)<=n-2时,最高阶非零子式的阶数<=n-2,任何n-1阶子式均为零,而伴随阵中的各元素就是n-1阶子式再加上个正负号,所以伴随阵为0矩阵。
当r(A)<=n-1时,最高阶非零子式的阶数<=n-1,所以n-1阶子式有可能不为零,所以伴随阵有可能非零(等号成立时伴随阵必为非零)。
矩阵秩为一有什么结论
秩等于1的矩阵是最无奈的情况,列那么多方程组,最后只有一个有用。伤不起