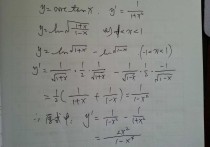什么时候用等价无穷小 求极限时常用的公式
在计算极限的时候,什么情况下可以用等价无穷小替换?能说明原因吗?请问什么时候可以用等价无穷小替换?求极限时什么时候适合用等价无穷小?什么时候可以用等价无穷小?只有是因子的时候可以等价么?请问什么时候能用等价无穷小,例如下图所示?等价无穷小什么时候用什么时候不能用?
本文导航
等价无穷小替换求极限的例题
等价无穷小一般只能在乘除中替换,在加减中替换有时会出错(加减时可以整体代换,不一定能随意单独代换或分别代换)。
求极限时,使用等价无穷小的条件:
1、被代换的量,在取极限的时候极限值为0;
2、被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
独立的乘积的因子若是无穷小,可以用等价的无穷小替换。例如lim(x→0) sinx*tanx/x^2,这里的sinx,tanx都可以替换,如果是lim(x→0) (sinx-tanx)/x^3,分子的sinx,tanx都不能替换,可以化成lim(x→0) tanx(cosx-1)/x^3后,替换sinx与1-cosx。
扩展资料:
当x→0时,等价无穷小:
(1)sinx~x
(2)tanx~x
(3)arcsinx~x
(4)arctanx~x
(5)1-cosx~1/2x^2
(6)a^x-1~xlna
(7)e^x-1~x
(8)ln(1+x)~x
(9)(1+Bx)^a-1~aBx
(10)[(1+x)^1/n]-1~1/nx
(11)loga(1+x)~x/lna
参考资料来源:百度百科-等价无穷小
等价无穷小能直接替换的条件
做为因数的时候能代换,或者如果替换的无穷小去掉之后,函数的极限依然存在的时候,就可以替换。
求极限时常用的公式
求极限时,使用等价无穷小的条件; ;:
1、被代换的量,在取极限的时候极限值为0;
2、被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
等价无穷小替换是计算未定型极限的常用方法,它可以使求极限问题化繁为简,化难为易。
扩展资料:;
利用极限四则运算法则求极限
函数极限的四则运算法则:设有函数,若在自变量f(x),g(x)的同一变化过程中,有limf(x)=A,limg(x)=B,则
lim[f(x)±g(x)]=limf(x)±limg(x)=A±B
lim[f(x)・g(x)]=limf(x)・limg(x)=A・B
lim==(B≠0)
(类似的有数列极限四则运算法则)现以讨论函数为例。对于和、差、积、商形式的函数求极限,自然会想到极限四则运算法则,但使用这些法则,往往要根据具体的函数特点,先对函数做某些恒等变形或化简,再使用极限的四则运算法则。
参考资料来源:百度百科-等价无穷小
什么情况下可以用等价无穷小替代
等价无穷小是指x趋于0(无穷小)时两个式子的变化快慢一致,即两个式子在x趋于0时相除得1.这时就叫等价无穷小。用等价无穷小的条件是“加减有条件,乘除无条件”
等价无穷小怎么判断
在只有乘除的极限中可以应用等价无穷小(大)
在有加减的极限中慎用等价无穷小(大)
在有加减的极限中用等价无穷小(大),如果这个无穷小(大)会被抵消,一般都可能出错,那就要考虑高阶的,所谓高阶,就是麦克劳林展式多取几项,究竟几项视情况而定
在有加减的极限中用等价无穷小(大),如果这个无穷小(大)不会被抵消,那么可能不出错,会与答案巧合,比如:(tanx-2sinx)/ln(1+x)~(x-2x)/x=-1
等价无穷小要上下都换吗
相关条件如下:
1、被代换的量,在取极限的时候极限值不为0。
2、被代换的量作为加减的元素时就不可以使用,作为被乘或者被除的元素时可以用等价无穷小代换。
等价无穷小是无穷小之间的一种关系,指的是:在同一自变量的趋向过程中,若两个无穷小之比的极限为1,则称这两个无穷小是等价的。无穷小等价关系刻画的是两个无穷小趋向于零的速度是相等的。
等价无穷小相关延伸:极限
数学分析的基础概念。它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的数值(极限值)。极限方法是数学分析用以研究函数的基本方法,分析的各种基本概念(连续、微分、积分和级数)都是建立在极限概念的基础之上,然后才有分析的全部理论、计算和应用。
所以极限概念的精确定义是十分必要的,它是涉及分析的理论和计算是否可靠的根本问题。历史上是柯西(Cauchy,A.-L.)首先较为明确地给出了极限的一般定义。他说,“当为同一个变量所有的一系列值无限趋近于某个定值,并且最终与它的差要多小就有多小”(《分析教程》,1821),这个定值就称为这个变量的极限。
其后,外尔斯特拉斯(Weierstrass,K.(T.W.))按照这个思想给出严格定量的极限定义,这就是数学分析中使用的ε-δ定义或ε-Ν定义等。从此,各种极限问题才有了切实可行的判别准则。在分析学的其他学科中,极限的概念也有同样的重要性,在泛函分析和点集拓扑等学科中还有一些推广。