二维概率怎么算 二维边缘概率密度函数的公式是怎么推导出来的?
二维概率密度计算,二维变量概率密度的计算,二维随机变量概率密度怎么求?二维边缘概率密度函数的公式是怎么推导出来的?关于二维随机变量(X,Y)的概率问题。
本文导航
二维概率密度计算
从黑字开始后面一个对v的积分的积分号本来应该是在最前面,但是前面对u的积分得到的结果(1-e^-x)与v无关,所以(1-e^-x)可以作为对v积分的系数,可以提前。
二维变量概率密度的计算
在长方形均区域匀分布,各自边缘分布符合均匀分布
1
X~U[0,2]
fx(x)=1/2 (0<=x<=2)
=0 (else)
2
f(x,y)=1/2 在所给方形区域
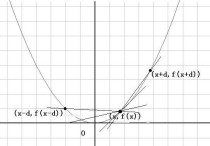
画图分析,画出x^2=y这条曲线,和x:[0,2] y:[0,1]的方形
P(X^2>Y)
=1-P(X^2<=Y)
=1-∫(0~1)∫(x^2~1) (1/2) dydx
=1-∫(0~1) (1-x^2)/2 dx
=1-(x/2-x^3/6 (0~1))
=1-(1/2-1/6)
=1-1/3
=2/3
二维随机变量概率密度怎么求
你好!将二元联合分布函数F(x,y)对x与y各求一次偏导数就得到联合概率密度函数。经济数学团队帮你解答,请及时采纳。谢谢!
二维边缘概率密度函数的公式是怎么推导出来的?
因为这个基本上只涉及到数学层面所以我就来问了,就是关于比如为什么求变量X的概率密度却对变量Y积分。
按照图里的样式,求关于x的偏导后,积分上下限和dx应该是变成1了吧,相当于将其消去了
关于二维随机变量(X,Y)的概率问题
可利用联合概率密度的二重积分为1,求出k=2。
边际密度函数的求解,本质就是考察积分,只要记住边缘概率密度就是对联合密度函数求积分,当我们求关于Y的边际密度函数时就是对于f(x,y)的联合密度函数关于X求积分,求Y的边际密度函数则同理。
第二部分是求随机变量函数的密度,一般用分布函数法,即先用定义求出分布函数,再求导得到相应的概率密度。
扩展资料:
注意事项:
连续随机变量的概率函数的导数就是概率密度函数,反过来,知道了概率密度函数就相当于知道了任意区间的随机事件的发生概率。
由于某个事件的概率是非负的,所以概率密度的取值也是非负,不过概率密度可以很大,也可以很小,且必须有区间作为参考和对比,单独分析一个点的概率密度是没有任何意义的。