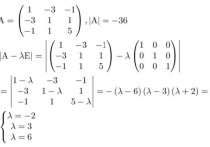矩阵的秩 什么是 矩阵的秩一般指的是行秩还是列秩
什么叫矩阵的秩?矩阵的秩是什么 麻烦讲得通俗易懂?矩阵的秩是什么?矩阵的“秩”是什么意思?怎么计算矩阵的“秩”?什么叫做矩阵的秩?怎么样求秩呢?什么是矩阵的秩?
本文导航
矩阵的秩是什么通俗易懂
矩阵的秩
矩阵的秩是反映矩阵固有特性的一个重要概念。
定义1. 在m´n矩阵A中,任意决定k行和k列 (1£k£min{m,n}) 交叉点上的元素构成A的一个k阶子矩阵,此子矩阵的行列式,称为A的一个k阶子式。
例如,在阶梯形矩阵 中,选定1,3行和3,4列,它们交叉点上的元素所组成的2阶子矩阵的行列式 就是矩阵A的一个2阶子式。
定义2. A=(aij)m×n的不为零的子式的最大阶数称为矩阵A
的秩,记作rA,或rankA。
特别规定零矩阵的秩为零。
显然rA≤min(m,n) 易得:
若A中至少有一个r阶子式不等于零,且在r<min(m,n)时,A中所有的r+1阶子式全为零,则A的秩为r。
由定义直接可得n阶可逆矩阵的秩为n,通常又将可逆矩阵称为满秩矩阵, det(A)¹ 0;不满秩矩阵就是奇异矩阵,det(A)=0。
由行列式的性质1(1.5[4])知,矩阵A的转置AT的秩与A的秩是一样的。
矩阵的秩一般指的是行秩还是列秩
就他妈是方程的个数,你平常解方程怎么解的,是不是就把两个方程相互加减啊,有的时候你把方程相加减最后你会发现有一对甚至更多的方程是一样的,这些一样的方程就等价于一个方程,然后加上其他的那些乱七八糟的方程,就是秩
矩阵的秩怎么判定
矩阵的秩就是行(列)向量组的极大无关组中向量的个数,
如果用初等行变换把矩阵化为上三角形,则就是非 0 的行数 。
什么是矩阵的秩
怎么看矩阵的秩为多少
矩阵的秩是反映矩阵固有特性的一个重要概念。
定义1.
在m´n矩阵A中,任意决定k行和k列
(1£k£min{m,n})
交叉点上的元素构成A的一个k阶子矩阵,此子矩阵的行列式,称为A的一个k阶子式。
例如,在阶梯形矩阵
中,选定1,3行和3,4列,它们交叉点上的元素所组成的2阶子矩阵的行列式
就是矩阵A的一个2阶子式。
定义2.
A=(aij)m×n的不为零的子式的最大阶数称为矩阵A
的秩,记作rA,或rankA。
特别规定零矩阵的秩为零。
显然rA≤min(m,n)
易得:
若A中至少有一个r阶子式不等于零,且在r<min(m,n)时,A中所有的r+1阶子式全为零,则A的秩为r。
由定义直接可得n阶可逆矩阵的秩为n,通常又将可逆矩阵称为满秩矩阵,
det(A)¹
0;不满秩矩阵就是奇异矩阵,det(A)=0。
矩阵秩的意义
矩阵的秩就是矩阵中最大非零子式的阶数
这种问题找本教材看看就行了, 直接问没什么用, 如果要问最好也是看过教材之后有针对性地提问