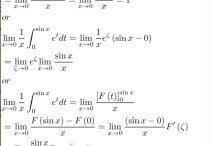什么是等价无穷小因子 常见等价无穷小的证明
如何确定一个高数题的等价无穷小因子?什么是等价无穷小?高数 考研 极限 无穷小因子 谢谢,常见的等价无穷小有哪些,等价无穷小的使用条件是什么?使用等价无穷小的条件是什么?
本文导航
高数等价无穷小替换公式怎么记住
判断书上应该很详细了。
比如要判断f(x)的无穷小阶数。就是看,当x->时,f(x)/x^a极限存在,则f(x)与x^a有相同的阶数。
当然用泰勒展开就可以明显的看出来,不过没有必要这么麻烦的去做。
这是最基本的判断方法,你也可以通过其他一些具体的途径去看。
比如x与sinx同阶,类似的还有很多。
要注意的是,无穷小的阶数(x->0时),与无穷大的阶数(x->无穷大时)不同,别搞混了。
你问的这几个很容易求,你就自己动动手。
等价无穷小在什么情况下可以用
这是高数中的 一般用来求解极限 比如 当x趋近于零时,sinx 和x 就是 那么当遇到sinx 比上x时 比值直接等于1 这些等价无穷小是要记住的
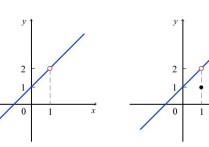
高数极限例题及图解
我理解的是:
A是B的无穷小因子的意思是B是A的等价无穷小,即当x趋向于0时,对B/A求极限=1。跟你说的带进去没什么关系吧
常见等价无穷小的证明
常见的等价无穷小的替换。
等价无穷小是怎么计算的
求极限时使用等价无穷小的条件:
1、被代换的量,在去极限的时候极限值为0。
2、被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
无穷小就是以数零为极限的变量。然而常量是变量的特殊一类,就像直线属于曲线的一种。确切地说,当自变量x无限接近某个值x0(x0可以是0、∞、或是别的什么数)时,函数值f(x)与零无限接近,即f(x)=0,则称f(x)为当x→x0时的无穷小量。
扩展资料:
数学分析的基础概念。它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的数值(极限值)。
极限方法是数学分析用以研究函数的基本方法,分析的各种基本概念(连续、微分、积分和级数)都是建立在极限概念的基础之上,然后才有分析的全部理论、计算和应用.所以极限概念的精确定义是十分必要的,它是涉及分析的理论和计算是否可靠的根本问题。
历史上是柯西(Cauchy,A.-L.)首先较为明确地给出了极限的一般定义。他说,“当为同一个变量所有的一系列值无限趋近于某个定值,并且最终与它的差要多小就有多小”(《分析教程》,1821),这个定值就称为这个变量的极限。
其后,外尔斯特拉斯(Weierstrass,K.(T.W.))按照这个思想给出严格定量的极限定义,这就是现在数学分析中使用的ε-δ定义或ε-Ν定义等。从此,各种极限问题才有了切实可行的判别准则。
在分析学的其他学科中,极限的概念也有同样的重要性,在泛函分析和点集拓扑等学科中还有一些推广。
常用等价无穷小的证明
求极限时使用等价无穷小的条件:
1、被代换的量,在去极限的时候极限值为0。
2、被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
无穷小就是以数零为极限的变量。然而常量是变量的特殊一类,就像直线属于曲线的一种。确切地说,当自变量x无限接近某个值x0(x0可以是0、∞、或是别的什么数)时,函数值f(x)与零无限接近,即f(x)=0,则称f(x)为当x→x0时的无穷小量。
扩展资料:
当x→0时,等价无穷小:
(1)sinx~x
(2)tanx~x
(3)arcsinx~x
(4)arctanx~x
(5)1-cosx~1/2x^2
(6)a^x-1~xlna
(7)e^x-1~x
(8)ln(1+x)~x
(9)(1+Bx)^a-1~aBx
(10)[(1+x)^1/n]-1~1/nx
极限的求法有很多种:
(1)连续初等函数,在定义域范围内求极限,可以将该点直接代入得极限值,因为连续函数的极限值就等于在该点的函数值。
(2)利用恒等变形消去零因子(针对于0/0型)。
(3)利用无穷大与无穷小的关系求极限。
(4)利用无穷小的性质求极限。
(5)利用等价无穷小替换求极限,可以将原式化简计算。
(6)利用两个极限存在准则,求极限,有的题目也可以考虑用放大缩小,再用夹逼定理的方法求极限。
(7)利用两个重要极限公式求极限。
(8)利用左、右极限求极限,(常是针对求在一个间断点处的极限值)。
参考资料来源:百度百科-等价无穷小