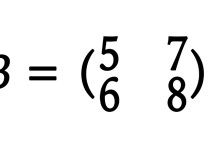矩阵对应的二次型什么意思 二次型怎样写成矩阵
高等代数矩阵二次型,矩阵里面的二次型是什么?线性代数。什么是二次型矩阵?请问用矩阵记号表示下列二次型是什么意思啊,比如下面这个题,该咋做啊?怎样用矩阵形式表示二次型?二次型的矩阵有什么特征?
本文导航
用矩阵形式表示二次型
对于二次型,矩阵A都是要求为实对称矩阵。
实对称矩阵可以对角化,就是说,存在可逆矩阵P,使得P^{-1}AP为对角矩阵,这里P^{-1}表示P的逆矩阵。
具体求法就如你所说,先求出A的特征根,以及分别对应各个根的特征向量,P1,P2,P3,此时令P=(P1,P2,P3),就满足P^{-1}AP为对角矩阵。
但是若想把P^{-1}变为PT,就要想办法把P变成正交阵,因为正交阵的定义就是逆和转置相同。
所以需要把P1,P2,P3正交单位化得Q1,Q2,Q3,这样得到的矩阵(Q1,Q2,Q3)就是正交阵。
注意:通常需要正交单位化而不是仅仅单位化,但是如果P1,P2,P3属于不同的特征根,则它们本身就是正交的,就可以省去正交化的过程。
二次型对应的矩阵一定是对称的吗
简单来说就是有两个未知元并且两个未知元的次数和为2
线性代数矩阵特征公式
就是对称矩阵的意思(因为二次型用对称阵来表示)
二次型怎样写成矩阵
二次型经过正交变换化为标准型,等价于将二次型矩阵相似变换为对角型矩阵,
由所给的标准型可知二次型矩阵相似变换为对角型的矩阵为diag(6,0,0).
再由相似的矩阵有相等的迹(矩阵的迹就是其主对角线上的元素之和)
而原二次型的矩阵的迹为a+a+a=3a
对角型的矩阵diag(6,0,0)的迹为6+0+0=6
得3a=6,所以a=2
线性代数二次型怎么写成矩阵
用矩阵形式表示二次型的方法:
二次型f(x,y,z)=ax²+by²+cz²+dxy+exz+fyz,用矩阵表示的时候,矩阵的元素与二次型系数的对应关系为:A11=a,A22=b,A33=c,A12=A21=d/2,A13=A31=e/2,A23=A32=f/2。
二次型的定义:
设f(x_1,x_2,...x_n)=∑a_ij
*
x_i*x_j
这里是系数,
满足aij=aji,则称f为n元二次型。
拓展资料
二次型:n个变量的二次多项式称为二次型,即在一个多项式中,未知数的个数为任意多个,但每一项的次数都为2的多项式。线性代数的重要内容之一,它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究。二次型理论与域的特征有关。
术语二次型也经常用来提及二次空间,它是有序对(V,q),这里的V是在域k上的向量空间,而q:V→k是在V上的二次形式。例如,在三维欧几里得空间中两个点之间的距离可以采用涉及六个变量的二次形式的平方根来找到,它们是这两个点的各自的三个坐标。
参考资料:搜狗百科-二次型
二次型的矩阵为什么都是对称的
用矩阵形式表示二次型的方法:
二次型f(x,y,z)=ax²+by²+cz²+dxy+exz+fyz,用矩阵表示的时候,矩阵的元素与二次型系数的对应关系为:A11=a,A22=b,A33=c,A12=A21=d/2,A13=A31=e/2,A23=A32=f/2。
二次型的定义:
设f(x_1,x_2,...x_n)=∑a_ij * x_i*x_j 这里是系数, 满足aij=aji,则称f为n元二次型。