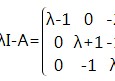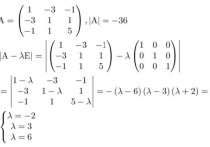哪些矩阵可对角化 怎样证明一个矩阵可对角化
矩阵对角化的方法都有哪些,下列矩阵中哪些矩阵可对角化?并对可对角化得矩阵A,求一个可逆矩阵P,使P^-1AP成对角矩阵,可对角化矩阵的介绍,矩阵可对角化的条件(3个,第4题中哪些矩阵可对角化?哪些矩阵不能对角化,下列矩阵中,哪些矩阵可以相似对角化……。
本文导航
什么是矩阵的对角化
我觉得应该是相似对角化吧,具体的步骤是:
1,求出一个矩阵的全部互异的特征值a1,a2……
2,对每个特征值,求特征矩阵a1I-A的秩,判断每个特征值的几何重数q=n-r(a1I-A),是否等于它的代数重数p,只要有一个不相等,A就不可 以相似对角化,否则, 就可以相似对角化
3,当可以相似对角化时,对每个特征值,求方程组,(aiI-A)X=0的一个基础解系
4,令P=这些基础解系,则P-1AP=diag(a1,a2,a3……),其中有qi个特征值
你看行不?
这就是我知道的,呵呵
怎样证明一个矩阵可对角化
通过求det(入E-A)=0 求出A的特征值为 3 ;2 ;-1
再通过Aa=入a a是入对应的特征向量;求出每个特征值对应的特征向量 后 假如这三个特征向量是a1 a2 a3 那么(a1 a2 a3)就是p矩阵
矩阵可对角化的简单判定
可对角化矩阵是线性代数和矩阵论中重要的一类矩阵。如果一个方块矩阵 A 相似于对角矩阵,也就是说,如果存在一个可逆矩阵 P 使得 P −1AP 是对角矩阵,则它就被称为可对角化的。如果 V 是有限维度的向量空间,则线性映射 T : V → V 被称为可对角化的,如果存在 V 的一个基,T 关于它可被表示为对角矩阵。对角化是找到可对角化矩阵或映射的相应对角矩阵的过程。可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理: 它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。若尔当-谢瓦莱分解表达一个算子为它的对角部分与它的幂零部分的和。
怎么看一个矩阵可对角化
1、阶矩阵可对角化的充分必要条件是有个线性无关的特征向量。若 阶矩阵定理2 矩阵 的属于不同特征值的特征向量是线性无关的。
2、若阶矩阵有个互不相同的特征值,则可对角化。
3、阶矩阵可对角化的充分必要条件是:每个特征值对应的特征向量线性无关的最大个数等于该特征值的重数(即的每个特征值对应的齐次线性方程组的基础解系所含向量个数等于该特征值的重数,也即的每个特征子空间的维数等于该特征值的重数)。
可对角化矩阵和映射在线性代数中有重要价值,因为对角矩阵特别容易处理: 它们的特征值和特征向量是已知的,并通过简单的提升对角元素到同样的幂来把一个矩阵提升为它的幂。
扩展资料:
若n阶矩阵A有n个不同的特征值,则A必能相似于对角矩阵。
说明:当A的特征方程有重根时.就不一定有n个线性无关的特征向量,从而未必能对角化。
设M为元素取自交换体K中的n阶方阵,将M对角化,就是确定一个对角矩阵D及一个可逆方阵P,使M=PDP-1。设f为典范对应于M的Kn的自同态,将M对角化,就是确定Kn的一个基,使在该基中对应f的矩阵是对角矩阵。
参考资料来源:百度百科——可对角化矩阵
怎么判断一个矩阵是否可以对角化
1.所有特征根都不相等,那么不用说,绝对可以对角化
2.有等根,只需要等根(也就是重特征值)对应的那几个特征向量是线性无关的,那么也可以对角化,如果不是,那么就不能了。