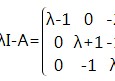矩阵特征值性质有哪些 特征值的结论
正定矩阵的特征及性质,矩阵的特征值与矩阵的哪些性质有关,矩阵的特征值的性质,如何理解矩阵特征值?特征值的性质是什么?矩阵的特征值。
本文导航
正定矩阵的例题讲解
矩阵正定性的性质:
1、正定矩阵的特征值都是正数。
2、正定矩阵的主元也都是正数。
3、正定矩阵的所有子行列式都是正数。
4、正定矩阵将方阵特征值,主元,行列式融为一体。
正定矩阵的特征方法:
1、 对称矩阵A正定的充分必要条件是A的n个特征值全是正数。
2、对称矩阵A正定的充分必要条件是A合同于单位矩阵E。
3、对称矩阵A正定(半正定)的充分必要条件是存在n阶可逆矩阵U使A=U^TU
4、对称矩阵A正定,则A的主对角线元素均为正数。
5、对称矩阵A正定的充分必要条件是:A的n个顺序主子式全大于零。
扩展资料:
一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z。
对于n阶实对称矩阵A,下列条件是等价的:
(1)A是正定矩阵;
(2)A的一切顺序主子式均为正;
(3)A的一切主子式均为正;
(4)A的特征值均为正;
(5)存在实可逆矩阵C,使A=C′C;
(6)存在秩为n的m×n实矩阵B,使A=B′B;
(7)存在主对角线元素全为正的实三角矩阵R,使A=R′R。
对于具体的实对称矩阵,常用矩阵的各阶顺序主子式是否大于零来判断其正定性;对于抽象的矩阵,由给定矩阵的正定性,利用标准型,特征值及充分必要条件来证相关矩阵的正定性。
参考资料来源:百度百科--正定矩阵
矩阵与其伴随矩阵的特征值关系
不知道你具体要问什么.如果是矩阵特征值是否有0,则与矩阵的秩有关,满秩矩阵没有0特征值;如果是矩阵的行列式,则行列式等于特征值的积;矩阵的迹等于特征值的和.
矩阵的特征值在哪讲
仅证A即可.
A是Hermite
矩阵,则A^H=A,A^H是A的共轭转置,
设a是A的任意特征值,x是相应特征向量,则
Ax=ax,两边取共轭转置得
x^HA^H=a*x^H,
其中a*是a的共轭复数,两边分别右乘x得
x^HAx=a*x^Hx,由Ax=ax得
ax^Hx=a*x^Hx
由x不为零,x^Hx不为零(>0),故a=a*,一个复数等于它的共轭复数,它必是实数,故a为实数.
矩阵特征值
:定义
设A是n阶方阵,如果数λ和n维非零列向量x使关系式
Ax=λx
(1)
成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量.(1)式也可写成,
(
A-λE)X=0
(2)
这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式
|
A-λE|=0
,
(3)
设
A
是n阶方阵,如果存在数m和非零n维列向量
x,使得
Ax=mx
成立,则称
m
是A的一个特征值(characteristic
value)或本征值(eigenvalue)。非零n维列向量x称为矩阵A的属于(对应于)特征值m的特征向量或本征向量,简称A的特征向量或A的本征向量。求矩阵特征值的方法:
Ax=mx,等价于求m,使得(mE-A)x=0,其中E是单位矩阵,0为零矩阵。
|mE-A|=0,求得的m值即为A的特征值。|mE-A|
是一个n次多项式,它的全部根就是n阶方阵A的全部特征值,这些根有可能相重复,也有可能是复数。如果n阶矩阵A的全部特征值为m1
m2
...
mn,则|A|=m1*m2*...*mn
同时矩阵A的迹是特征值之和:tr(A)=m1+m2+m3+…+mn[1]
如果n阶矩阵A满足矩阵多项式方程g(A)=0,
则矩阵A的特征值m一定满足条件g(m)=0;特征值m可以通过解方程g(m)=0求得。还可用mathematica求。
矩阵的特征值意味什么
设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。
式Ax=λx也可写成( A-λE)X=0,这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式| A-λE|=0。
矩阵特征值的性质:
若λ是可逆阵A的一个特征根,x为对应的特征向量,则1/λ 是A的逆的一个特征根,x仍为对应的特征向量。
若 λ是方阵A的一个特征根,x为对应的特征向量,则λ 的m次方是A的m次方的一个特征根,x仍为对应的特征向量。
特征值的结论
特征值的性质是指矩阵A的行列式的值为所有特征值的积,矩阵A的对角线元素和称为A的迹等于特征值的和。
特征值和特征向量确实有很明确的几何意义,矩阵(既然讨论特征向量的问题,当然是方阵,这里不讨论广义特征向量的概念,就是一般的特征向量)乘以一个向量的结果仍是同维数的一个向量。因此,矩阵乘法对应了一个变换,把一个向量变成同维数的另一个向量。
变换的效果:
这当然与方阵的构造有密切的关系,比如可以取适当的二维方阵,使得这个变换的效果就是将平面上的二维变量逆时针旋转30度。
这时,我们可以思考一个问题,有没有向量在这个变换下不改变方向。可以想一下,除了零向量,没有其他向量可以在平面上旋转30度而不改变方向的,所以这个变换对应的矩阵(或者说这个变换自身)没有特征向量(注意,特征向量不能是零向量)。
矩阵的特征值有什么用
设A是n阶方阵,如果存在数m和非零n维列向量;x,使得 Ax=mx 成立,则称 m 是矩阵A的一个特征值或本征值。
式Ax=λx也可写成( A-λE)X=0。这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式| A-λE|=0。
相关内容:
矩阵特征值
性质1:若λ是可逆阵A的一个特征根,x为对应的特征向量,则1/λ 是A的逆的一个特征根,x仍为对应的特征向量。
性质2:若 λ是方阵A的一个特征根,x为对应的特征向量,则λ 的m次方是A的m次方的一个特征根,x仍为对应的特征向量。
性质3:设λ1,λ2,…,λm是方阵A的互不相同的特征值。xj是属于λi的特征向量( i=1,2,…,m),则x1,x2,…,xm线性无关,即不相同特征值的特征向量线性无关。