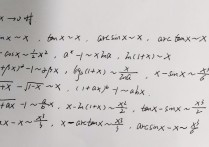泰勒公式需要什么条件 泰勒公式展开后怎么求极限
泰勒公式求极限有什么前提条件?泰勒公式的使用条件,泰勒公式的使用条件是x趋向于0,请问泰勒公式的使用条件是什么?怎么判断泰勒公式的展开式应该展开到哪一项?泰勒公式的使用条件是什么?
本文导航
泰勒公式展开后怎么求极限
如果你是用麦克劳林公式,就必须要在x->0的情况下可用
例如,你要用sin(1/x)的麦克劳林公式,则必须1/x->0
泰勒公式常见问题
可以,u=1/x趋于零,u的泰勒展开
x=0时的泰勒公式
首先,泰勒公式没有对于自变量取值的使用条件,只是我们常用x在0附近的泰勒展开,其又称为麦克劳林公式。麦克劳林公式是解析函数在0附近的幂级数表达式,与x从那个方向趋向于0无关。因为对于一个解析函数,只要x在0附近,都可以麦克劳林展开,而不管x在0附近的变化情况。所以不论x从哪个方向趋向于0,都不影响泰勒公式的使用条件(注意其本质原因是泰勒公式的使用条件根本上就与x如何取值无关,而在于函数是否连续可导;只不过我们常用在0点附近的展开,但x如何趋向于0本就不是判断泰勒公式能否使用的条件,希望不要弄混)。
打字不易,拒绝复粘,希望采纳!
泰勒展开式十个常用公式
实际应用中,泰勒公式需要截断,只取有限项,一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用于估算这种近似的误差。
泰勒展开式的重要性体现在以下三个方面:
幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。
泰勒级数可以用来近似计算函数的值。
使用泰勒公式有要求吗
结果是1,不能用泰勒公式。
泰勒公式是将一个在x=x₀处具有n阶导数的函数f(x)利用关于(x-x₀)的n次多项式来逼近函数的方法。
若函数f(x)在包含x₀的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有(n+1)阶导数,则对闭区间[a,b]上任意一点x,成立下式:
其中,表示f(x)的n阶导数,等号后的多项式称为函数f(x)在x₀处的泰勒展开式,剩余的Rₙ(x)是泰勒公式的余项,是(x-x₀)ⁿ的高阶无穷小。
扩展资料:
余项
泰勒公式的余项Rₙ(x)可以写成以下几种不同的形式:
1、佩亚诺(Peano)余项:
2、施勒米尔希-罗什(Schlomilch-Roche)余项:
参考资料来源:百度百科-泰勒公式