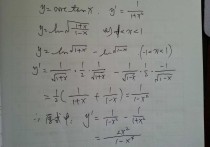怎么证明导数可导 怎么证明函数可导，详细的说法

怎么证明函数可导，详细的说法？如何证明某函数可导？怎样证明一个函数在一个区间内可导？怎么证明函数可导性？如何证明导数可导？如何证明函数处处可导？

本文导航

• 怎么证明函数可导，详细的说法
• 如何证明某函数可导？
• 怎样证明一个函数在一个区间内可导？
• 怎么证明函数可导性
• 如何证明导数可导？
• 如何证明函数处处可导？

怎么证明函数可导，详细的说法

初等函数在定义域内都可导，其他函数按照定义求

对分段函数要分别求左右导数，如果存在且相等才可导

如何证明某函数可导？

函数在定义域中一点可导需要一定的条件：函数在该点的左右导数存在且相等，不能证明这点导数存在。只有左右导数存在且相等，并且在该点连续，才能证明该点可导。可导的函数一定连续；连续的函数不一定可导，不连续的函数一定不可导。

如果一个函数在x0处可导，那么它一定在x0处是连续函数。

函数可导定义：

（1）设f(x)在x0及其附近有定义,则当a趋向于0时,若 [f(x0+a)-f(x0)]/a的极限存在, 则称f(x)在x0处可导。

（2）若对于区间(a,b)上任意一点m，f(m)均可导，则称f(x)在(a，b)上可导。

扩展资料

导数计算的原则和方法

1、原则：先化简解析式，使之变成能用八个求导公式求导的函数的和、差、积、商再求导．

2、方法：

①连乘积形式：先展开化为多项式的形式，再求导；

②分式形式：观察函数的结构特征，先化为整式函数或较为简单的分式函数，再求导；

③对数形式：先化为和、差的形式，再求导；

④根式形式：先化为分数指数幂的形式，再求导；

⑤三角形式：先利用三角函数公式转化为和或差的形式，再求导；(理)

⑥复合函数：由外向内，层层求导。

参考资料来源：百度百科-可导

怎样证明一个函数在一个区间内可导？

1、证明函数在整个区间内连续。（初等函数在定义域内是连续的）

2、先用求导法则求导，确保导函数在整个区间内有意义。

3、端点和分段点用定义求导。

4、分段点要证明左右导数均存在且相等。

如果y在x=x0处左右导数分别存在且相等,则称y在x=x[0]处可导。如果一个函数在x0处可导，那么它一定在x0处是连续函数。

扩展资料：

如果一个函数的定义域为全体实数，函数在定义域中一点可导需要一定的条件：函数在该点的左右导数存在且相等，不能证明这点导数存在。只有左右导数存在且相等，并且在该点连续，才能证明该点可导。

可导的函数一定连续；连续的函数不一定可导，不连续的函数一定不可导。

函数与不等式和方程存在联系（初等函数）。令函数值等于零，从几何角度看，对应的自变量的值就是图像与X轴的交点的横坐标。

从代数角度看，对应的自变量是方程的解。另外，把函数的表达式（无表达式的函数除外）中的“=”换成“<”或“>”，再把“Y”换成其它代数式，函数就变成了不等式，可以求自变量的范围。

参考资料来源：百度百科--可导

怎么证明函数可导性

分两步证明。

第一步证明函数在任意点是连续的。

第二步证明函数在任意一点的左右极限存在，并且相等。

欢迎采纳。。。谢谢

如何证明导数可导？

　　初等函数的可导性已经在教材中证明了，不需要你来证明，直接计算就是。只有非初等函数（如分段函数）才需要证明其（如在分段点的）可导性。

如何证明函数处处可导？

用定义证明：

对任意x0∈R，任意ε>0，总存在正数d，使对所有|x-x0|<d，有|f(x)-f(x0)|<ε。

则f(x)在R上处处连续。

对任意x0∈R，有lim(x->x0)[f(x)-f(x0)]/(x-x0)存在，则f(x)在R上处处可导。

充分必要条件：

函数可导的充要条件：函数在该点连续且左导数、右导数都存在并相等。

函数可导与连续的关系，函数可导则函数连续；函数连续不一定可导；不连续的函数一定不可导。