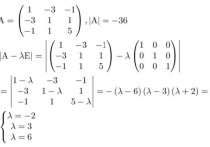可对角化矩阵长什么样 矩阵的可对角化条件
如何判断一个矩阵是否可对角化?如何判断一个矩阵是否可以相似对角化?如何判断一个矩阵是否可对角化??可对角化的矩阵通常都有哪些。
本文导航
如何证明一个矩阵可以对角化
将矩阵A的特征多项式完全分解, 求出A的特征值及其重数,若k重特征值都有k个线性无关的特征向量,则A可对角化。否则不能对角化。
举例说明:
看这个矩阵是否能对角化,暂且把这个定义成A矩阵。
需要用到一个公式,如下图所示,我们这一步就是直接按照公式套入就可以了。
把上一步得到的结果进行整理,结果是一个行列式。然后按照展开法则进行展开。
得出这个算式的指,也就是这个行列式的特征根。
对这两个根进行讨论,然后求出来基础解系,然后我们根据基础解系来判断是否能够进行对角化。
如何快速看出一个矩阵能否对角化
1-存在可逆矩阵p,使得p-1Ap=对角阵
2-有n个线性无关的特征向量
3-最小多项式可分解为互素一次因式的乘积
4-初等因子都是一次的
5-每个特征值的重数等于对应特征子空间的维数
6-属于不同特征值的特征子空间的维数之和等于n
7-存在一个零化多项式可分解成互素一次因式的乘积
矩阵的可对角化条件
n级矩阵a可对角化<=>a的属于不同特征值的特征子空间维数之和为n.
实际判断方法:(1)先求特征值,如果没有相重的特征值,一定可对角化;
(2)如果有相重的特征值λk,其重数为k,那么你通过解方程(λke-a)x=0得到的基础解系中的解向量若也为k个,则a可对角化,若小于k,则a不可对角化.
此外,实对称矩阵一定可对角化.
你可以对照课本上的例题或习题.