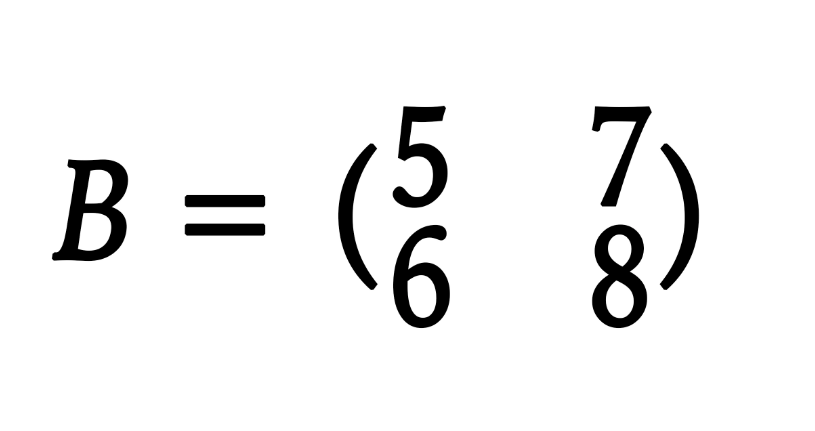什么矩阵的特征向量正交 特征向量相互正交则满足什么公式
如何判断特征向量是否正交?实对称矩阵相同特征值的特征向量相互正交吗?实对称矩阵相同特征值对应的特征向量正交吗?
本文导航
特征向量相互正交则满足什么公式
将两向量做内积,得出结果为0则两特征向量正交。
例子:
设向量m=(x1,x2,x3),n=(y1,y2,y3)那么m*n=x1y1+x2y2+x3y3如果m*n=0,那么称m和n正交。
特征向量性质:
线性变换的特征向量是指在变换下方向不变,或者简单地乘以一个缩放因子的非零向量。
特征向量对应的特征值是它所乘的那个缩放因子。
特征空间就是由所有有着相同特征值的特征向量组成的空间,还包括零向量,但要注意零向量本身不是特征向量。
线性变换的主特征向量是最大特征值对应的特征向量。
特征值的几何重次是相应特征空间的维数。
有限维向量空间上的一个线性变换的谱是其所有特征值的集合。
二阶实对称矩阵快速求特征值
实对称矩阵相同特征值的特征向量不一定相互正交。例如:n×n阶单位矩阵E是实对称矩阵,且任何n维向量都是E的特征向量,但不能说任何两个n维向量都是正交的,属于单位阵E的某个特征值的特征向量有的相互正交,也有的不相互正交。
实对称矩阵的主要性质:
1、实对称矩阵A的不同特征值对应的特征向量是正交的。
2、实对称矩阵A的特征值都是实数,特征向量都是实向量。
3、n阶实对称矩阵A必可对角化,且相似对角阵上的元素即为矩阵本身特征值。
4、若λ具有k重特征值 必有k个线性无关的特征向量,或者说必有秩r(λE-A)=n-k,其中E为单位矩阵。
扩展资料:
正交矩阵的相关性质
1、方阵A正交的充要条件是A的行(列)向量组是单位正交向量组;
2、方阵A正交的充要条件是A的n个行(列)向量是n维向量空间的一组标准正交基;
3、A是正交矩阵的充要条件是:A的行向量组两两正交且都是单位向量;
4、A的列向量组也是正交单位向量组;
5、正交方阵是欧氏空间中标准正交基到标准正交基的过渡矩阵。
参考资料来源:百度百科-实对称矩阵
实对称矩阵的特征值怎么计算
实对称矩阵不同特征值的特征向量一定是正交的。实对称矩阵同一特征值的不同特征向量线性无关。结论很明显,书上解释得也很清楚,我猜题主问这个问题是对于下面这个问题的疑惑。这里说的是存在,并没有说对于实对称矩阵A的特征值分解,得到的U一定是正交矩阵。而是可以采用一些正交化方法使得U成为正交矩阵,就是说即使U不是正交矩阵,但U的各列向量线性无关。
矩阵:
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。