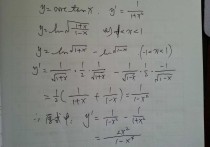泰勒公式展开式怎么用 如何用泰勒公式展开 看题
怎么用泰勒展开式展开In(1+x?如何用泰勒公式展开 看题?泰勒公式是怎么展开的?或者说展开的计算是怎么得到的?泰勒公式的用法。
本文导航
怎么用泰勒展开式展开In(1+x)
如图:(注意“麦克劳林级数”是“泰勒级数”的特殊形式,是展开位置为0的泰勒级数)。
一阶导数,系数=1/(x+1)=1/(1+x0)。二阶导数,系数=-1/(1+x)^2=-1/(1+x0)^2
数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
扩展资料
实际应用中,泰勒公式需要截断,只取有限项,一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用于估算这种近似的误差。
泰勒展开式的重要性体现在以下五个方面:
1、幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
2、一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。
3、泰勒级数可以用来近似计算函数的值,并估计误差。
4、证明不等式。
5、求待定式的极限。
如何用泰勒公式展开 看题
## 泰勒公式
计算各阶导数后代入泰勒公式即可推导出展开式,熟练了则可直接心算/背出
泰勒公式是怎么展开的?或者说展开的计算是怎么得到的?
这个是在0处展开,所以原泰勒公式中的a
都取0,那么sin展开式中的系数就变为0或者1了。
是让a取0,不是x取0
泰勒公式的用法?
实际应用中,泰勒公式需要截断,只取有限项,一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用于估算这种近似的误差。 泰勒展开式的重要性体现在以下五个方面: 幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。 一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。 泰勒级数可以用来近似计算函数的值,并估计误差。 证明不等式。 求待定式的极限。
; ; ; ; ; ;
; ; ; ; ; ;
拓展资料
一、中值定理
由导数的定义可知,当函数 在点处可导时,在点的邻域内有 ;因为 是一个无穷小量,故有 。这是在对函数进行局部线性化处理时常用的公式之一。从几何上看,它是用切线来代替曲线的。然而,这样的近似是比较粗糙的,而且只在点的附近才有近似的意义为了改善上述不足,使得近似替代更加精密,数学家们在柯西中值定理的基础上,推导出了泰勒中值定理(泰勒公式) 。
; ; ; ; ; ;
二、公式余项
泰勒公式的余项有两类:一类是定性的皮亚诺余项,另一类是定量的拉格朗日余项。这两类余项本质相同,但是作用不同。一般来说,当不需要定量讨论余项时,可用皮亚诺余项(如求未定式极限及估计无穷小阶数等问题);当需要定量讨论余项时,要用拉格朗日余项(如利用泰勒公式近似计算函数值) ;。
; ; ; ; ; ;
三、几何意义
泰勒公式的几何意义是利用多项式函数来逼近原函数,由于多项式函数可以任意次求导,易于计算,且便于求解极值或者判断函数的性质,因此可以通过泰勒公式获取函数的信息,同时,对于这种近似,必须提供误差分析,来提供近似的可靠性。
四、一元公式
一个通用表达式,根据拉格朗日中值定理导出的有限增量定理有,其中误差是在,即的前提下才趋于0,在近似计算中往往不够精确。
五、多元公式
除了一元泰勒公式外,多元泰勒公式的应用也非常广泛,特别是在微分方程数值解和最优化上有着很大的作用 ;。
; ; ; ; ; ;