数学定积分怎么算 定积分怎么计算？

高数 定积分 请问怎么算啊？定积分怎么求？高数定积分怎么求？高数，求解定积分的怎么算？定积分怎么算出来的？定积分怎么计算？

本文导航

• 高数 定积分 请问怎么算啊
• 定积分怎么求
• 高数定积分怎么求
• 高数，求解定积分的怎么算？
• 定积分怎么算出来的？
• 定积分怎么计算？

高数 定积分 请问怎么算啊

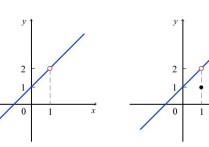
那就是一个数，只要积分区间是确定的数，并且被积函数的所有变量都参与积分，那所得的值就是一个数。

题中所说的是一元函数的积分，并且积分区间是[0,1]，从而该积分就是一个数。这是因为：

设∫f(x)dx=F(x),则题中的积分结果就是 F(1)-F(0)，这当然就是一个数。

定积分怎么求

高数定积分怎么求

简单计算一下即可，答案如图所示

高数，求解定积分的怎么算？

换元法，加分部积分法

设√x=t，t=0~π/2，x=t²，dx=2tdt

∫cos√xdx

=∫2tcostdt

=2∫tdsint

=2[tsint-∫sintdt]

=2[tsint+cost]

积分=2[tsint+cost]（0，π/2）

=π-2

定积分怎么算出来的？

本题关键就是：对ln根号x的积分计算需要利用到分部积分法，其余的按照定积分规则计算即可。解法如图所示：

定积分怎么计算？

定积分可以使用“分项积分法”进行计算。

如一个函数在不同的定义域有不同的表达式，那么表达式一样的函数，也可以分成一段段的来表示积分，当然前提要满足函数的可积法。

定积分的几何定义：可以理解为在 Oxy坐标平面上，由曲线y=f(x)与直线x=a，x=b以及x轴围成的曲边梯形的面积值（一种确定的实数值）。

首先分析积分区间是否关于原点对称，其次考虑被积函数是否具有周期性，再次考察被积函数是否可以转换为“反对幂指三”五类基本函数中两个类型函数的乘积，或者是否包含有正整数n参数，或者包含有抽象函数的导数乘项等。

分析积分区间是否关于原点对称，即为[-a,a]，如果是，则考虑被积函数的整体或者经过加减拆项后的部分是否具有奇偶性，如果有，则考虑使用“偶倍奇零”性质简化定积分计算。

考虑被积函数是否具有周期性，如果是周期函数，考虑积分区间的长度是否为周期的整数倍，如果是，则利用周期函数的定积分在任一周期长度的区间上的定积分相等的结论简化积分计算。

考察被积函数是否可以转换为“反对幂指三”五类基本函数中两个类型函数的乘积，或者是否包含有正整数n参数，或者包含有抽象函数的导数乘项，如果是，可考虑使用定积分的分部积分法计算定积分。