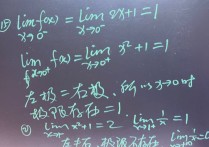数学的极限怎么求 数学求极限的方法
数学上怎么求无穷比无穷型的极限?数学求极限的方法,对于数学,判断是否存在极限的,要怎么求呢?高等数学,求极限。要详细过程最好手写谢谢,数学求极限。
本文导航
求无穷大或者无穷小极限的方法
方法一:都是幂指数的形式,可以提出最高次项,极限值就是最高次项的系数之比,如下图所示。
方法二:可以用洛必达法则求极限。具体做法是同时对分子分母求导,然后借助方法一或者直接代入,可以得到答案。。
拓展资料
洛必达法则:对于0/0型或者无穷/无穷型求极限的问题,可以对分子分母同时求导,极限值不变。这个法则就是洛必达法则。
运用条件:保证求导一个分子、分母以及分式极限存在,否则洛必达法则失效。
数学求极限的方法
去你们学校数科院,找个学生,要本数学分析的习题集,百度写不下也不想写。
对于数学,判断是否存在极限的,要怎么求呢?
无论对于何种极限,只要其附近的所有有取值的点的值足够接近,或者其本身的取值足够接近一个值,有那么该点处就存在极限。
不过对于上句话里附近、有取值的点、足够接近,这些词在不同的数学阶段有不同的定义,比如高中的定义就会宽泛得多,到了数学分析里就会给出严格的定义。
无论是序列的极限,函数的极限,上极限和下极限,网的极限,拓扑空间中的极限点等等,都是这样一个基本的意思,简而言之就是有其他点的取值不断的向那个点逼近。
由此可见,极限这个概念的主体一般是一个序列或者一个集合。
这样一来,我们就可以明确如何判断以及如何求极限,考察是否有序列或集合逼近就是判断极限是否存在的关键,而逼近的程度或者说逼近到的取值点就是求极限的关键。
不过请注意,上一花福羔凰薏好割瞳公困段话里的逼近、序列以及集合等词也都在不同的数学阶段有着严格度不同的定义,在数学分析,泛函分析以及拓扑学中的定义是最严格的,也是有具体的数学含义的。
高等数学,求极限。要详细过程最好手写谢谢
当x一>0时,分子和分母皆一>0,这是0/0型未定式,符合洛必达法则的条件,对分子和分母分别求导,整理,代入x=0,求出分式函数的极限为1。
本题还可以应用等价无穷小的摡念,当x一>时,分子ln(1+x)~x,分母e^x-1~x,用等价无穷小代换之在,原分式函数的极限就等于x/x=1的极限,根据常数的极限还是常数,也就是无论x怎么变化,函数的值都不变。
数学求极限
如图: