导数与微分有什么差别 微分公式和导数公式有什么联系
导数与微分有什么区别?求真相?导数和微分有什么本质区别?导数和微分的区别,微分就是求导吗?微分和求导有什么区别呀?微分和求导有什么区别?
本文导航
微分是求导数吗
对一个函数积分和对它微分,这两个运算互为逆运算。 求原函数的过程是不定积分运算;求导的过程是微分运算。 一个函数的微分与它的导数也略有区别,微分是函数的线性增量(变化),而导数是函数的变化率(也就是函数值变化/自变量变化)。
导数与微分简单理解方法
导数反映变化快慢,微分反应变化增量。
没有本质区别,只是表现形式不一样
导数与微分关系
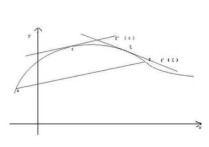
导数是函数图像在某一点处的斜率,也就是纵坐标增量(Δy)和横坐标增量(Δx)在Δx-->0时的比值。微分是指函数图像在某一点处的切线在横坐标取得增量Δx以后,纵坐标取得的增量,一般表示为dy。
导数是函数图像在某一点处的斜率,也就是纵坐标变化率和横坐标变化率的比值。微分是指函数图像在某一点处的切线在横坐标取得Δx以后,纵坐标取得的增量。
扩展资料
微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。微积分的基本概念之一。
定义:
设函数y = f(x)在x的邻域内有定义,x及x + Δx在此区间内。
如果函数的增量Δy = f(x + Δx) - f(x)可表示为 Δy = AΔx + o(Δx)(其中A是不依赖于Δx的常数),而o(Δx)是比Δx高阶的无穷小(注:o读作奥密克戎,希腊字母)那么称函数f(x)在点x是可微的,且AΔx称作函数在点x相应于因变量增量Δy的微分,记作dy,即dy = AΔx。
函数的微分是函数增量的主要部分,且是Δx的线性函数,故说函数的微分是函数增量的线性主部(△x→0)。
参考资料
百度百科-微分
微分和导数的区别通俗
微分不是求导。
1、定义不同
微分:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。
求导:当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。
2、基本法则不同
微分:基本法则
求导:基本求导公式
给出自变量增量;;;
得出函数增量;;;
作商;;;
求极限;;。
3、应用不同
微分:法线,我们知道,曲线上一点的法线和那一点的切线互相垂直,微分可以求出切线的斜率,自然也可以求出法线的斜率。
增函数与减函数,微分是一个鉴别函数(在指定定义域内)为增函数或减函数的有效方法。
变化的速率,微分在日常生活中的应用,就是求出非线性变化中某一时间点特定指标的变化。
求导:求导是微积分的基础,同时也是微积分计算的一个重要的支柱。物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。
参考资料:百度百科-求导
参考资料:百度百科-微分
微分公式和导数公式有什么联系
1、本质不同
求导:当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。
微分:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。
2、比值增量的不同
导数:函数图像在某一点处的斜率,也就是纵坐标增量(Δy)和横坐标增量(Δx)在Δx-->0时的比值。
微分:函数图像在某一点处的切线在横坐标取得增量Δx以后,纵坐标取得的增量,一般表示为dy。
微积分,数学概念,是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。
扩展资料:
微分在日常生活中的应用,就是求出非线性变化中某一时间点特定指标的变化。
例如,水箱中充满了水,水箱里水的体积V(升)和时间t(秒)的关系为V=5-2/(t+1),
当t=3时,想知道此时的加水率,所以在t=3后计算dV/dt=2/(t+1)^2,代入t=3后得出dV/dt=1/8。
因此,可以得出结论,水箱中的水量在充水3秒开始时以每秒1/8升的速度增加。
参考资料来源:百度百科-求导
参考资料来源:百度百科-微分
参考资料来源:百度百科-微积分