什么是数项级数 级数通俗解释
数项级数,数项级数和幂级数的区别是什么?级数是什么意思?什么是数级?数即包括,哪个级?函数项级数是什么?
本文导航
正项级数与常数项级数的区别
n趋向于无穷时(-1)^(n-1){1/2^n-1}的绝对值的极限=0
而且各项符号交错,所以级数收敛。
1-1/2+1/4-1/8+……+(-1)^n-1{1/2^n-1}……
=lim(n→∞)[1-(-1/2)^n]/[1-(-1/2)]
=2/3
这是一个等比数列求和,首项是1,公比是-1/2,不过他有无穷多项,所以求和实际就是求n→∞时的极限。
当n→∞时(-1/2)^n的极限是0。
所以整个极限=(1-0)/[1-(-1/2)]=2/3
数项级数的基本概念
数项级数和幂级数的区别是什么
数项级数的每一项都是数
幂级数的每一项都是幂函数.
级数通俗解释
级数是指将数列的项依次用加号连接起来的函数。典型的级数有正项级数、交错级数、幂级数、傅里叶级数等。
级数理论是分析学的一个分支;它与另一个分支微积分学一起作为基础知识和工具出现在其余各分支中。二者共同以极限为基本工具,分别从离散与连续两个方面,结合起来研究分析学的对象,即变量之间的依赖关系──函数。
级数怎么划分的
级数是指将数列的项依次用加号连接起来的函数。典型的级数有正项级数、交错级数、幂级数、傅里叶级数。
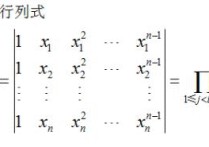
如将数列 Un的项 U1 , U2 ,U3…, Un ,…依次用加号连接起来的函数,是数项级数的简称。
U1+U2+U3+...+Un+...记作西格马Un,Un为级数的通项。
高数级数的总结
函数项级数:在数学中,一个有穷或无穷的序列的元素的形式和称为级数。序列中的项称作级数的通项。级数的通项可以是实数,矩阵或向量等常量,也可以是关于其他变量的函数,不一定是一个数。如果级数的通项是常量,则称之为常数项级数,如果级数的通项是函数,则称之为函数项级数。
对函数列的求和就是函数项级数,而把函数项级数的每一项拿出来组成的一列函数,就是函数列。
函数发展历史:
1,函数的由来
(1)中文数学书上使用的“函数”一词是转译词。是我国清代数学家李善兰在翻译《代数学》(1859年)一书时,把“function”译成“函数”的。
(2)中国古代“函”字与“含”字通用,都有着“包含”的意思。李善兰给出的定义是:“凡式中含天,为天之函数。”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量。这个定义的含义是:“凡是公式中含有变量x,则该式子叫做x的函数。”所以“函数”是指公式里含有变量的意思。
2,早期概念
(1)1637年前后笛卡尔在他的解析几何中,已注意到一个变量对另一个变量的依赖关系,但因当时尚未意识到要提炼函数概念,因此直到17世纪后期牛顿,莱布尼兹建立微积分时还没有人明确函数的一般意义,大部分函数是被当作曲线来研究的。
(2)1673年,莱布尼兹首次使用“function”(函数)表示“幂”,后来他用该词表示曲线上点的横坐标,纵坐标,切线长等曲线上点的有关几何量。与此同时,牛顿在微积分的讨论中,使用 “流量”来表示变量间的关系。