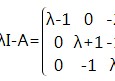重根变换矩阵怎么求 求帮忙，怎么将矩阵化为约当标准型，那个变化矩阵P怎么求

矩阵特征值的初等变换求法，常微分方程中有重根的矩阵怎么求特征向量？求帮忙，怎么将矩阵化为约当标准型，那个变化矩阵P怎么求？线性代数中特征方程有重根怎么求基础解系？知道特征值和特征向量怎么求矩阵？三阶矩阵三重根怎么求基础解系？

本文导航

• 矩阵特征值的初等变换求法
• 常微分方程中有重根的矩阵怎么求特征向量
• 求帮忙，怎么将矩阵化为约当标准型，那个变化矩阵P怎么求
• 线性代数中特征方程有重根怎么求基础解系?
• 知道特征值和特征向量怎么求矩阵
• 三阶矩阵三重根怎么求基础解系

矩阵特征值的初等变换求法

首先，并不是对每一个A都能找到对角的B的。

其次，对于矩阵A，若能找到对角的B和某一个可逆的P，使得PAP^(-1)=B的，称A可对角化，其中B对角线上元素就是A的特征值,(重根按重数算)，P的列向量就是A的n个线性无关的特征向量，并且要与B中特征值的排列次序对应。

再次，对于不能对角化的，也就是找不到n个线性无关特征向量的，最后不能利用相似变换化为对角形，只能化到若当标准形，就是由若当块组成的准对角，这个时候PAP^(-1)=J，J为若当标准形，这个时候P的列向量就不完全是A的特征向量了，它的组成要由A的特征值的情况来定。

这个是不可能完全做到的，要是让你完全做到了，任意多项式的求根问题就被你解决了，而这个是已经被证明不可能做到的。所以个人认为使用相似变换求特征值的方法应该只有数值方法，不会有理论上的求解析解的方法。

常微分方程中有重根的矩阵怎么求特征向量

常微分方程中哪有矩阵的概念？

线性代数中，有重根和没有重根，求特征向量的第一步是一样的。

就是(A-sE)x=0求解

如果解得的特征向量数不够，再计算

(A-sE)(A-sE)x=0

求帮忙，怎么将矩阵化为约当标准型，那个变化矩阵P怎么求

首先必须求最小多项式。一般只要矩阵不特殊都是sI-A初等行列变换变成史密斯标准型，从而通过行列式因子或者直接算出来不变因子组，写成(x-si)^ni形式后，求初等因子组，初等因子组里相同因子方幂最大的相乘就得到了最小多项式。例如我们求得初等...

线性代数中特征方程有重根怎么求基础解系?

有重根，只把重根代入特征方程一次，然后求出基础解系，即可得到属于这个重根的特征向量

知道特征值和特征向量怎么求矩阵

对于特征值λ和特征向量a，得到Aa=aλ

于是把每个特征值和特征向量写在一起

注意对于实对称矩阵不同特征值的特征向量一定正交

得到矩阵P，再求出其逆矩阵P^(-1)

可以解得原矩阵A=PλP^(-1)

设A为n阶矩阵，若存在常数λ及n维非零向量x，使得Ax=λx，则称λ是矩阵A的特征值，x是A属于特征值λ的特征向量。

一个矩阵A的特征值可以通过求解方程pA(λ) = 0来得到。 若A是一个n×n矩阵，则pA为n次多项式，因而A最多有n个特征值。

反过来，代数基本定理说这个方程刚好有n个根，如果重根也计算在内的话。所有奇数次的多项式必有一个实数根，因此对于奇数n，每个实矩阵至少有一个实特征值。在实矩阵的情形，对于偶数或奇数的n，非实数特征值成共轭对出现。

扩展资料

求矩阵的全部特征值和特征向量的方法如下：

第一步：计算的特征多项式；

第二步：求出特征方程的全部根，即为的全部特征值；

第三步：对于的每一个特征值，求出齐次线性方程组。

若是的属于的特征向量，则也是对应于的特征向量，因而特征向量不能由特征值惟一确定．反之，不同特征值对应的特征向量不会相等，亦即一个特征向量只能属于一个特征值。

在A变换的作用下，向量ξ仅仅在尺度上变为原来的λ倍。称ξ是A 的一个特征向量，λ是对应的特征值（本征值），是（实验中）能测得出来的量，与之对应在量子力学理论中，很多量并不能得以测量，当然，其他理论领域也有这一现象。

三阶矩阵三重根怎么求基础解系

要理解特征多项式，首先需要了解一下特征值与特征向量，这些都是联系在一起的：

设A是n阶矩阵，如果数λ和n维非零列向量x使得关系式Ax=λx成立，那么，这样的数λ就称为方阵A的特征值，非零向量x称为A对应于特征值λ的特征向量。

也就可以对关系式进行变换：

(A-λE)x=0 其中E为单位矩阵

这是n个未知数n个方程的齐次线性方程组，它有非零解的充要条件是系数行列式为0，即|A-λE|=0

带入具体的数字或者符号，可以看出该式是以λ为未知数的一元n次方程，称为方阵A的特征方程，左端 |A-λE|是λ的n次多项式，也称为方阵A的特征多项式。到此为止，特征多项式的定义表述完毕。

扩展资料：

设A是数域P上的一个n阶矩阵，λ是一个未知量，系数行列式|A-λE|称为A的特征多项式，记¦(λ)=|λE-A|，是一个P上的关于λ的n次多项式，E是单位矩阵。

¦(λ)=|λE-A|=λn+a1λn-1+…+an= 0是一个n次代数方程，称为A的特征方程。特征方程¦(λ)=|λE-A|=0的根(如：λ0)称为A的特征根(或特征值)。n次代数方程在复数域内有且仅有n个根，而在实数域内不一定有根，因此特征根的多少和有无，不仅与A有关，与数域P也有关。

参考资料来源：百度百科-矩阵特征值