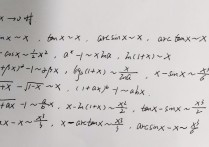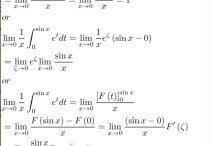函数连续性怎么判断 如何简单判断一个函数是否连续
如何简单判断一个函数是否连续?怎么判断一个函数是连续函数?高数中。连续性和可导性怎么判断?如何判断函数是否连续和可导呢?
本文导航
如何简单判断一个函数是否连续
根据函数的连续性定义来判断。
函数连续性定义:
对定义域内任意一个x0,在x0的领域内都有limf(x)=f(x0)(x->x0)
即函数在x0处的极限值等于该点的函数值时,由函数在该点连续,如果函数在定义域内的每一个点都连续,则该函数在定义域内连续。
从图像上看,函数连续,则图像是一条不断开的曲线。如果从某点处断开,则函数在该点就不连续了。
怎么判断一个函数是连续函数
初等函数在其定义域的任意子区间都连续。
高数中。连续性和可导性怎么判断
1.函数的连续性定义有三个条件
f(x)在x=x0点有定义;f(x)在x→x0时极限存在;极限值等于函数值
此外,还有个命题
基本初等函数在其定义域中连续,初等函数在其定义区间中连续。
因此,判断函数的连续性,一般先观察函数是否为初等函数(由基本初等函数经过有限次四则运算以及复合而成的函数),如果是,那么在它的定义区间上的每一点都是连续的!
如果函数是个分段函数,那么先考虑每个分段上的连续性,然后考虑分段点的连续性,采用的方法依据定义来判断!
2.函数的可导性主要是考虑极限lim
Δy/Δx=lim
[f(x)-f(x0)]/(x-x0)是否存在的问题.
对于基本初等函数,它们也都是在它的定义域中可导的。
如果碰到分段函数,记得分段点的可导性一定要用定义来判断!
此外,对于一元函数来讲,可导必连续,反之未必成立!
如何判断函数是否连续和可导呢?
一个函数在某一区间上连续(可导)指的是该函数在此区间的任意一点上连续(可导)。
至于判断在某一点上函数是否连续或可导,即判断某个极限是否存在。
判断函数f在点x0处是否连续,即判断极限lim(x--x0)f(x)是否存在且等于f(x0)。
判断函数f在点x0处是否可导,即判断极限lim(dx--0)(f(x+dx)-f(x))/dx是否存在。
对于连续性,在自然界中有许多现象,如气温的变化,植物的生长等都是连续地变化着的。这种现象在函数关系上的反映,就是函数的连续性。
设函数;;在点;;的某个邻域内有定义,如果有;;,则称函数在点;;处连续,且称;为函数的的连续点。
一个函数在开区间;;内每点连续,则为在;;连续,若又在;;点右连续,;;点左连续,则在闭区间;;连续,如果在整个定义域内连续,则称为连续函数。
显然,由极限的性质可知,一个函数在某点连续的充要条件是它在该点左右都连续。
扩展资料:
如果f是在x0处可导的函数,则f一定在x0处连续,特别地,任何可导函数一定在其定义域内每一点都连续。反过来并不一定。事实上,存在一个在其定义域上处处连续函数,但处处不可导。
间断有以下三种情况:
1.在点;;处;;没有定义,在;;为发散状态(y=tanx在x=kπ+π/2处无定义,并且在x=kπ+π/2处发散到无穷大);
2.在;;无定义,趋近与;;时连续波动(y=sin(1/x)在x=0处无定义,并且在0的某个去心邻域内无限振荡);
3.虽然;;有定义,且;;存在,但不等于;;(分段函数在x=0处的左右极限都存在,但不等于f(0))。
参考资料:百度百科——可导函数
参考资料:百度百科——连续函数