正态分布怎么计算期望值 正态分布的期望值和方差是什么?
正态分布期望如何算?正态分布的数学期望推导过程!希望拍照啊,请问概率论中正态分布的数学期望如何求出?其中有一步不太懂。。。希望大神指点?正态分布的期望值和方差是什么?正态分布的公式是什么?正态分布的期望是什么?
本文导航
- 正态分布期望如何算
- 正态分布的数学期望推导过程!希望拍照啊!
- 请问概率论中正态分布的数学期望如何求出?其中有一步不太懂。。。希望大神指点
- 正态分布的期望值和方差是什么?
- 正态分布计算公式表
- 正态分布的期望是什么?
正态分布期望如何算
如果有公式,不要算,就是u
如果是一堆数,比如,[1,2,,3,2,3,3,4,4,5,4,5,6](N=12)近似正态,可以这样算:
N1 = 1*(1出现次数/N) = 1;
N2 = 2*(2出现次数/N)=2*2/12 = 0.3333
N3 = ...
最后期望是:N1+N2+N3+.....N6 = ...
正态分布的数学期望推导过程!希望拍照啊!
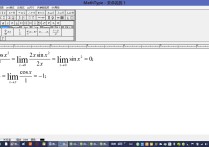
第三行是拆开以后第一项奇0得到的
请问概率论中正态分布的数学期望如何求出?其中有一步不太懂。。。希望大神指点
标准正态分布期望不是0嘛→_→
首先被积函数是个奇函数,积分区间又是对称的,所以应该是0而不是其他的
正态分布的期望值和方差是什么?
求期望:ξ
期望:Eξ=x1p1+x2p2+……+xnpn
方差:s²
方差公式:s²=1/n[(x1-x)²+(x2-x)²+……+(xn-x)²]
注:x上有“-”
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布。
正态分布计算公式表
正态分布函数密度曲线可以表示为:称x服从正态分布,记为X~N(m,s2),其中μ为均值,s为标准差,X∈(-∞,+ ∞ )。标准正态分布另正态分布的μ为0,s为1。
扩展资料
正态分布符号定义
若随机变量X服从一个数学期望为μ、方差为的高斯分布,记为N(μ,)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。正态分布有两个参数,即均数(μ)和标准差(σ)。
μ是位置参数,当σ固定不变时, μ越大,曲线沿横轴,越向右移动;反之, μ越小,则曲线沿横轴,越向左移动。是形状参数,当μ固定不变时,σ越大,曲线越平阔;σ越小,曲线越尖峭。通常用表示标准正态分布。
参考资料来源:百度百科-正态分布
正态分布的期望是什么?
正态分布的期望是:Eξ。
正态分布的期望用数学符号表示ξ,所以正态分布的期望的公式是:Eξ=x1p1+x2p2+……+xnpn,而方差用数学符号表示s,所以正态分布的方差的公式是:s=1/n[(x1-x)+(x2-x)+……+(xn-x)],另外x上有“-”。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
方差:
样本中各数据与样本平均数的差的平方和的平均数为样本方差;样本方差的算术平方根为样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。
方差和标准差为测算离散趋势最重要、最常用的指标,它是测算数值型数据离散程度的最重要的方法。标准差为方差的算术平方根,用S表示。