第一类曲线积分是什么 第一类曲线积分的计算例题及解析
关于第一类曲线积分,第一类曲线积分,这一段怎么看呢?第一类曲线积分怎么求?第一类曲线积分和第二类曲线积分的异同,第一类曲线积分的几何意义,第一类曲线积分计算方法。
本文导航
第二类曲线积分的定义
第一类是对弧长积分,即定义在弧长上,没有方向.如求非密度均匀的线状物体质量。第二类是对坐标(有向弧长在坐标轴的投影)积分,有方向.如解决做功类问题。假设曲线正向,两者可互换,弧长元dscosθ=dx,dssinθ=dy,(cosθ,sinθ)是沿着正向曲线单位切向量。
第一类曲线积分的计算例题及解析
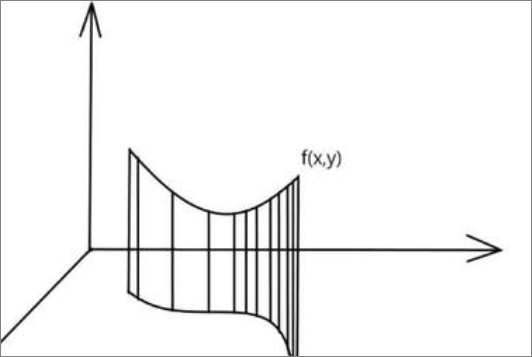
这是第一类曲线积分,圆圈代表积分曲线是封闭曲线。曲线积分分为:对弧长的曲线积分 (第一类曲线积分),对弧长的曲线积分和对坐标轴的曲线积分是可以互相转化的,利用弧微分公式ds=√[1+(dy/dx)^2]*dx;或者ds=√[1+(dx/dy)^2]*dy;这样对弧长的曲线积分都可以转换成对坐标轴的曲线积分了。
设有一曲线形构件占xOy面上的一段曲线 ,设构件的质量分布函数为ρ(x,y),设ρ(x,y)定义在L上且在L上连续,求构件的质量。对于密度均匀的物件可以直接用ρS求得质量;对于密度不均匀的物件,就需要用到曲线积分,dm=ρ(x,y)ds;所以m=∫ρ(x,y)ds;L是积分路径,∫ρ(x,y)ds就叫做对弧长的曲线积分。
第二类曲线积分计算法
设有一曲线形构件占xOy面上的一段曲线 ,设构件的密度分布函数为ρ(x,y),设ρ(x,y)定义在L上且在L上连续,求构件的质量。对于密度均匀的物件可以直接用ρV求得质量;
对于密度不均匀的物件,就需要用到曲线积分,dm=ρ(x,y)ds;所以m=∫ρ(x,y)ds;L是积分路径,∫ρ(x,y)ds就叫做对弧长的曲线积分。
扩展资料
量子力学
量子力学中的“曲线积分形式”和曲线积分并不相同,因为曲线积分形式中所用的积分是函数空间上的泛函积分,即关于空间中每个路径的概率函数进行积分。然而,曲线积分在量子力学中仍有重要作用,比如说复围道积分常常用来计算量子散射理论中的概率振幅。
复分关系
如果将复数看作二维的向量,那么二维向量场的曲线积分就是相应复函数的共轭函数在同样路径上的积分值的实部。根据柯西-黎曼方程,一个全纯函数的共轭函数所对应的向量场的旋度是0。
第二类曲线积分基本计算步骤
1、积分对象不同
第一类曲线积分是对弧长积分,对弧长的曲线积分的积分元素是弧长元素;
第二类曲线积分是对坐标(有向弧长在坐标轴的投影)积分,对坐标轴的曲线积分的积分元素是坐标元素。
2、应用场合不同
第一类曲线积分求非密度均匀的线状物体质量等问题;
第二类曲线积分解决做功类等问题。
3、是否考虑方向
第一类曲线积分都是和方向无关的,对标量的积分;
第二类曲线积分都是和方向有关的,对某种意义上的矢量的积分。
扩展资料
积分联系
对弧长的曲线积分和对坐标轴的曲线积分是可以互相转化的,利用弧微分公式
,或者
;这样对弧长的曲线积分都可以转换成对坐标轴的曲线积分了。
在曲线积分中,被积的函数可以是标量函数或向量函数。积分的值是路径各点上的函数值乘上相应的权重(一般是弧长,在积分函数是向量函数时,一般是函数值与曲线微元向量的标量积)后的黎曼和。
带有权重是曲线积分与一般区间上的积分的主要不同点。物理学中的许多简单的公式(比如说)在推广之后都是以曲线积分的形式出现。曲线积分在物理学中是很重要的工具,例如计算电场或重力场中的做功,或量子力学中计算粒子出现的概率。
参考资料来源:百度百科--曲线积分
参考资料来源:百度百科--第一型曲线积分
参考资料来源:百度百科--第二型曲线积分
空间曲线的第一类曲线积分公式
第一类曲线积分的几何意义:∫x^2ds=∫y^2d。在数学中,曲线积分是积分的一种。积分函数的取值沿的不是区间,而是特定的曲线,称为积分路径。曲线积分有很多种类,当积分路径为闭合曲线时,称为环路积分或围道积分。曲线积分可分为:第一类曲线积分和第二类曲线积分。
曲线,是微分几何学研究的主要对象之一。直观上,曲线可看成空间质点运动的轨迹。微分几何就是利用微积分来研究几何的学科。为了能够应用微积分的知识,我们不能考虑一切曲线,甚至不能考虑连续曲线,因为连续不一定可微。这就要我们考虑可微曲线。
怎么计算一型曲线积分
定义在平面曲线或空间曲线上的函数关于该曲线的积分。第一型曲线积分物理意义来源于对给定密度函数的空间曲线,计算该曲线的质量。1、对弧长的曲线积分(第一类)(1)如果L由y=y(x)给出,x属于[a,b]
[公式]
(2)如果L由x=x(y)给出,y属于[c,d],
[公式]
(3)如果L由[公式],[公式]
[公式]
2、对坐标的曲线积分(第二类)
(1)如果L由y=y(x)给出,x属于[a,b]
[公式]
(2)如果L由x=x(y)给出,y属于[c,d],
[公式]
(3)如果L由[公式],[公式]
[公式]
好了,只是贴个公式,就占用了那么多篇幅,看来计算公式真的够冗长的。其实大家仔细观察上面的公式,无论第一型曲线积分还是第二型曲线积分,都只需要记住第三种情况就行了,因为前两种都是第三种的特殊形式。那么这就是今天我要介绍的简单方法??哈哈,当然不是,我要介绍的比这个还简单。