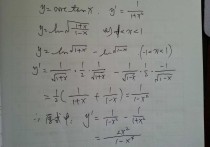函数不连续怎么求积分 不连续函数的定积分
不连续函数的定积分,这个不连续函数的能不能求定积分?求解,求教:高数积分问题不连续函数一定不可积,当定积分函数在积分区间不连续时,怎么求?例:∫(-1到1)1/xdx=?高等数学问题。不连续的函数,比如有跳跃间断点,它是否可积? 如果它可积,那它的变上限积分是否连续。
本文导航
- 不连续函数的定积分
- 这个不连续函数的能不能求定积分?求解
- 求教:高数积分问题不连续函数一定不可积
- 当定积分函数在积分区间不连续时,怎么求?例:∫(-1到1)1/xdx=?
- 高等数学问题。不连续的函数,比如有跳跃间断点,它是否可积? 如果它可积,那它的变上限积分是否连续?
不连续函数的定积分
恩,我也觉得题目答案错了。
半圆面积π/2,另一段的积分应该是e^x|<1,2>=e^2-e,
我的答案和你一样。
这个不连续函数的能不能求定积分?求解
通常所说的可积的定义是指黎曼可积,即任意区间分割的积分结果都要求是有界的并且极限相同。
因此你给的函数分成左右正负两个区间单独积分都不收敛,即定积分不存在。
求教:高数积分问题不连续函数一定不可积
y=积分 sec x dx
=ln|secx+tanx|+C
代入x=2,y=3
C=3-ln|sec2+tan2|
y=ln|secx+tanx|+3-ln|sec2+tan2|
2.
y=积分 cos^2 x sinx dx ,u=cosx, du=-sinxdx
=积分 u^2(-du)
=-u^3/3+C
=-cos^3 x /3 +C
代入x=0,y=-1
-1=-1/3+C
C=-2/3
y=-cos^3 x /3-2/3
当定积分函数在积分区间不连续时,怎么求?例:∫(-1到1)1/xdx=?
拆为两个积分,-1到0一个,另一个是0到1,然后两个积分均发散,本题结果是发散.
被积函数在积分区域内存在趋于无穷的点,这种积分称为瑕积分,属于广义积分的一种,不是通常的定积分.
高等数学问题。不连续的函数,比如有跳跃间断点,它是否可积? 如果它可积,那它的变上限积分是否连续?
有跳跃间断点的函数的变上限积分函数连续的。变上限积分函数应该出现的是类似于|x|这样分段的函数,分段点连续,但是不可导的情况。
所以如果是有第二类间断点,如无穷间断点,震荡间断点,是有可能(但也只是有可能,不是一定)不可积。而如果是有限个第一类(无论是跳跃间断点,还是可去间断点),都必然是可积的。
函数可积的充分条件:
1、定理1设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
2、定理2设f(x)在区间[a,b]上有界,且只有有限个第一类间断点,则f(x)在[a,b]上可积。
3、定理3设f(x)在区间[a,b]上单调有界,则f(x)在[a,b]上可积。
可积函数的有界
任何一个可积函数一定是有界的,但是需要注意的是,有界函数不一定可积。在其定义域上的每一点都不连续的函数。狄利克雷函数是处处不连续函数的一个例子。
若f(x)为一函数,定义域和值域都是实数,若针对每一个x,都存在ε>0 ,使得针对每一个δ>0,都可以找到y,使下式成立,则f(x)为处处不连续函数:0< |x−y|<δ 且|f(x)−f(y)|≥ε。