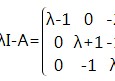矩阵特征值代表什么关系 如何理解矩阵的特征值和特征向量
如何理解矩阵特征值?矩阵和它的行列式,特征向量,特征值之间的关系是什么?一个矩阵的特征值和它的奇异值有什么关系?矩阵的秩与特征值有什么关系?矩阵的特征值和矩阵对应的行列式是啥关系,矩阵的秩和特征值有什么关系?
本文导航
如何理解矩阵的特征值和特征向量
从线性空间的角度看,在一个定义了内积的线性空间里,对一个N阶对称方阵进行特征分解,就是产生了该空间的N个标准正交基,然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基,而特征值的模则代表矩阵在每个基上的投影长度。特征值越大,说明矩阵在对应的特征向量上的方差越大,功率越大,信息量越多。
(1)应用到最优化中,意思就是对于R的二次型,自变量在这个方向上变化的时候,对函数值的影响最大,也就是该方向上的方向导数最大。
(2)应用到数据挖掘中,意思就是最大特征值对应的特征向量方向上包含最多的信息量,如果某几个特征值很小,说明这几个方向信息量很小,可以用来降维,也就是删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用信息量变化不大。
矩阵的秩与特征值有什么关系
矩阵A是方阵时,有行列式|A|
令|λI-A|=0
解出特征值λ
再把特征值,分别代入特征方程(λI-A)x=0
解出基础解系,即可得到特征向量
矩阵特征值与矩阵阶数的关系
奇异矩阵是线性代数的概念,
就是对应的行列式等于0的方阵。
那么现在|a|=0,
显然对应的特征值式子|a-ae|=0
当然有特征值a=0
矩阵的特征向量个数与秩的关系
1、方阵A不满秩等价于A有零特征值。
2、A的秩不小于A的非零特征值的个数。
线性变换秩是多少,就一定找到有多少个线性无关的特征向量。因为一个特征向量只能属于一个特征值,所以有多少个线性无关的特征向量,就有多少个特征值(不管特征值是不是一样)。这里有n个1,都是一样的(从特征多项式也知道有n个重根)。因为非退化的线性替换不改变空间的维数,不改变矩阵的秩。
扩展资料:
求矩阵的全部特征值和特征向量的方法如下:
1、第一步:计算的特征多项式;
2、第二步:求出特征方程的全部根,即为的全部特征值;
3、第三步:对于的每一个特征值,求出齐次线性方程组:的一个基础解系,则的属于特征值的全部特征向量是(其中是不全为零的任意实数)。
参考资料来源:百度百科-矩阵的秩
参考资料来源:百度百科-特征值
矩阵的秩和特征值个数有什么关系
矩阵A是方阵时,有行列式|A|,令|λI-A|=0,解出特征值λ。
一个特征空间就是一个由所有特征向量组成的空间它们有相同的特征值,包括0向量,但是注意到0向量本身不是特征向量是很重要的。
线性变换的主特征向量是对应于最大特征值的特征向量。特征值的几何多重性是对应特征空间的维数。有限维向量空间上的线性变换的谱是它所有特征值的集合。
扩展资料:
作为时间的函数,如果=0,它保持不变,如果是正的,它成比例地增加,如果是负的,它成比例地减少。例如,理想化的兔子总数在兔子多的地方繁殖得更快,这就满足了一个特征值方程。
特征值方程的一个解是N=exp(t),也称为指数函数;因此,该函数是特征值为的微分算子d/dt的特征函数。如果是负的,我们称N的演化为指数衰减。
特征矩阵的秩和原矩阵的秩一样吗
关系:如果矩阵可以对角化,那么非0特征值的个数就等于矩阵的秩;如果矩阵不可以对角化,这个结论就不一定成立了。
为讨论方便,设A为m阶方阵。
证明:设方阵A的秩为n。
如将特征值的取值扩展到复数领域,则一个广义特征值有如下形式:Aν=λBν。
其中A和B为矩阵。其广义特征值(第二种意义)λ 可以通过求解方程(A-λB)ν=0,得到det(A-λB)=0(其中det即行列式)构成形如A-λB的矩阵的集合。其中特征值中存在的复数项。
若是的属于的特征向量,则也是对应于的特征向量,因而特征向量不能由特征值惟一确定。反之,不同特征值对应的特征向量不会相等,亦即一个特征向量只能属于一个特征值。