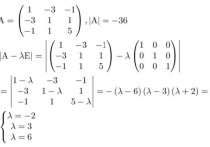对角矩阵怎么求 怎么算出对角矩阵的?
正交矩阵求出后怎么计算对角矩阵?这个对角矩阵是怎么求的?求对角矩阵,怎么算出对角矩阵的?对角矩阵求法,对角矩阵怎么求?
本文导航
正交矩阵求出后怎么计算对角矩阵?
直接得到,你得到的正交矩阵时P=(a1,a2,..,an)的话
对应的对角矩阵为diag(λ1,λ2,...,λn)
其中λi 为ai对应的特征值。
这个对角矩阵是怎么求的
对角矩阵的元素就是矩阵A的特征值所构成的
求对角矩阵
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
扩展资料1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。
2、矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
基本性质
乘法结合律: (AB)C=A(BC)
乘法左分配律:(A+B)C=AC+BC
乘法右分配律:C(A+B)=CA+CB
对数乘的结合性k(AB)=(kA)B=A(kB)
转置 (AB)T=BTAT.
矩阵乘法一般不满足交换律。
怎么算出对角矩阵的?
对角矩阵的值就是矩阵A的特征值,和Q的列向量一一对应,因为Q(正交矩阵)是通过特征值对应的特征向量单位化或正交化得来的,这和相似对角化的原理一样,特征值和特征向量是需要一一对应的。
对角矩阵求法
求对角矩阵的方法:求出一个矩阵的全部互异的特征值a1。a2。对每个特特征值,求特征矩阵a1I-A的秩。当可以相似对角化时,对每个特征值,求方程组,(aiI-A)X=0的一个基础解系。
对角矩阵(diagonal matrix)是一个主对角线之外的元素皆为0的矩阵,常写为diag(a1,a2,...,an) 。对角矩阵可以认为是矩阵中最简单的一种,值得一提的是:对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且结果仍为对角阵。
推论:
若n阶矩阵A有n个不同的特征值,则A必能相似于对角矩阵。
说明:当A的特征方程有重根时.就不一定有n个线性无关的特征向量,从而未必能对角化。
只有对角线上有非0元素的矩阵称为对角矩阵,或说若一个方阵除了主对角线上的元素外,其余元素都等于零,则称之为对角阵。
主对角线上方元素都为零的方阵,称为下三角阵。
对角阵既是上三角阵,又是下三角阵。
矩阵的对角线有许多性质,如做转置运算时对角线元素不变、相似变换时对角线的和(称为矩阵的迹)不变等。在研究矩阵时,很多时候需要将矩阵的对角线上的元素提取出来形成一个列向量,而有时又需要用一个向量构造一个对角阵。
对角矩阵怎么求
对角矩阵的公式是设M=(αij)为n阶方阵。M的两个下标相等的所有元素都叫做M的对角元素,而序列(αii)(1≤i≤n)叫做M的主对角线。对角矩阵是一个主对角线之外的元素皆为0的矩阵。对角线上的元素可以为0或其他值。