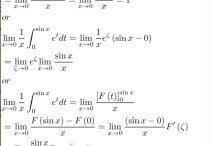极限怎么等价代换 关于极限等价
关于极限等价,极限的等价代换,求极限什么时候能等价代换? 如何快速正确判断?高数极限等价代换,函数极限问题,等价代换的用法,求极限的等价代换公式。
本文导航
关于极限等价
当x→0时,常用的等价无穷小有如下:
sinx~x~tanx~(e^x-1)~ln(1+x)
(1-cosx)~(1/2)x^2
[(1+x)^a-1]~ax
(x-sinx)~(1/6)x^3
以上是较为常用的代换。
如何确定是否该使用等价代换:
当X->0+或X->0或X->0-时,如果需要代换的部分(用f(x)表示)f(x)→0,那么f(x)就可以进行对应的代换。
一般来说,只有当f(x)作为所求表达式的一个因子的时候,可以用相应代换;那么特殊的情况下,f(x)与所求表达式是加减关系时,不一定不能用代换,但是加减关系用代换的错误率极大,一般初学高等数学的同学无法准确把握,建议加减不用代换。
另:代换中更一般的处理:
当x→0时,f(x)→0,那么有如下:
sinf(x)~f(x)~tanf(x)~(e^f(x)-1)~ln(1+f(x))
(1-cosf(x))~(1/2)[f(x)]^2
[(1+f(x))^a-1]~af(x)
(f(x)-sinf(x))~(1/6)f(x)^3
具体你的问题:
一般在求解极限时,要每做一步都要看看有没有极限是常数的因子;cos(x^2) 就是极限为1的因子,应该果断将其拿到极限号外,将表达式简化,再继续向下做。
极限的等价代换
等价,即两者的比极限为1
求极限什么时候能等价代换? 如何快速正确判断?
其实,在国际的微积分理论体系中,没有把等价无穷小代换作为一种方法;
它仅仅只是我们国内教学中的一种鱼目混珠、偷梁换柱、张冠李戴的方法;
它是将麦克劳林级数、泰勒级数展开的第一项窃取而来的投机取巧的方法;
.
由于它没有独立的、自洽的、完整的自身的理论体系,仅仅只是窃取而已,
所以,运用时等价无穷小代换时,经常出错是在所难免、无可避免的。
.
为了防止出错,我们加进了自残、自虐、自宫的条款:
【在有加减运算时,等价无穷小代换不可以使用】。
其实这句话是矫枉过正,是此地无银三百两的伎俩,是做贼心虚者的不打自招。
麦克劳林级数、泰勒级数并无此限制,无论如何加减乘除、如何复合都可使用。
.
所以,只要记住:
在有加减运算时,使用等价无穷小代换要特别谨慎,很容易出错。
在有加减运算时,可能会消除掉本来应该残留下来的高阶无穷小。
.
虽然自残条款,武断地排除了有可能能使用的情况,但是却避免了过多的差错。
是宁可不用,也害怕出错。实质是心虚,是底气不足。
.
在有加减运算时,建议楼主用泰勒展开、麦克劳林展开,万无一失。
而泰勒级数、麦克劳林级数,在国内的教学中,是刻意混为一谈的。
.
高数求极限的等量替换公式
注意你所谓的“等价变换”是偷换了概念,你的做法不是等价的!!因为,分子部分,如果说只有这三项的任意一项的话,完全没问题;但这是一个和,就不行了,因为和的等价形式是不知道的(除非你能证明)。事实上,根据泰勒展式,把每一项展开前几项,具体到哪一项,应考虑分母是几次方。
函数极限问题,等价代换的用法
如下
求极限的等价代换公式
求极限的等价代换公式
当x→0时,sinx-x,tanx-x,arcsinx-x,arctanx-x,1-cosx-(1/2)*(x^2)-secx-1,(a^x)-1-x*lna((a^x-1)/x-lna)、(e^x)-1-x等等。
极限是微积分和数学分析的其他分支最基本的概念之一,连续和导数的概念均由其定义。它可以用来描述一个序列的指标愈来愈大时,序列中元素的性质变化的趋势,也可以描述函数的自变量接近某一个值的时候,相对应的函数值变化的趋势。
性质分析
学习微积分学,首要的一步就是要理解到,“极限”引入的必要性:因为,代数是人们已经熟悉的概念,但是,代数无法处理“无限”的概念。所以为了要利用代数处理代表无限的量,于是精心构造了“极限”的概念。在“极限”的定义中,我们可以知道,这个概念绕过了用一个数除以0的麻烦,而引入了一个过程任意小量。
除数不是零,所以有意义,同时,这个过程小量可以取任意小,只要满足在Δ的区间内,都小于该任意小量,我们就说他的极限为该数——你可以认为这是投机取巧,但是,他的实用性证明,这样的定义还算比较完善,给出了正确推论的可能。这个概念是成功的。