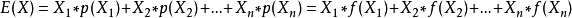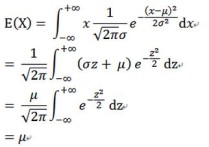二维数学期望怎么算 什么是数学期望?如何计算?
数学期望 怎么算?连续性二维随机变量数学期望,什么是数学期望?如何计算?二维随机变量已知概率密度,求期望方差,概率论 二维期望的求法,二维条件数学期望怎么求?
本文导航
数学期望 怎么算
分离散型R.V.和连续型R.V.。同时还有一维和二维之分。举个例子来说明吧
x a b c (一维离散型)
p 0.1 0.8 0.1
则:EX=0.1a+0.8b+0.1c
(一维连续型)设概率密度为:f(x) a<x<b
则,EX=∫<a,b>xf(x)dx
二维类似,碰上题了可以来问我
连续性二维随机变量数学期望
①求E(X),先求出X的边缘分布密度函数fX(x)。根据定义,fX(x)=∫(-∞,∞)f(x,y)fy=∫(0,∞)e^(-x-y)dy=[e^(-x)]∫(0,∞)e^(-y)dy=e^(-x)。
②按定义求期望值。E(X)=∫(0,∞)xfX(x)dx=∫(0,∞)xe^(-x)dx=1。
E(X+Y)=∫(0,∞)∫(0,∞)(x+y)e^(-x-y)dxdy==∫(0,∞)∫(0,∞)xe^(-x-y)dxdy+∫(0,∞)∫(0,∞)y e^(-x-y)dxdy=2。
E[e^(-x)]=∫(0,∞)[e^(-x)]fX(x)dx=∫(0,∞)e^(-2x)dx=1/2。
供参考。
什么是数学期望?如何计算?
数学期望是试验中每次可能结果的概率乘以其结果的总和。
计算公式:
1、离散型:
离散型随机变量X的取值为X1、X2、X3……Xn,p(X1)、p(X2)、p(X3)……p(Xn)、为X对应取值的概率,可理解为数据X1、X2、X3……Xn出现的频率高f(Xi),则:
2、连续型:
设连续性随机变量X的概率密度函数为f(x),若积分绝对收敛,则称积分的值
为随机变量的数学期望,记为E(X)。即
扩展资料例题:
在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,;;求:
(1)取出的3件产品中一等品件数x的分布列和数学期望;
(2)取出的3件产品中一等品件数多于二等品件数的概率。
解:
x的数学期望E(x)=0*7/24+1*21/40+2*7/40+3*1/120=9/10
参考资料来源:百度百科-数学期望
二维随机变量已知概率密度,求期望方差
概率密度:f(x)=(1/2√π)exp{-(x-3)²/2*2}
根据题中正态概率密度函数表达式就可以立马得到随机变量的数学期望和方差:
数学期望:μ=3
方差:σ²=2
连续型随机变量的概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。
而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
扩展资料:
连续随机变量在任意点的概率为0。作为推论,连续随机变量在某一区间上的概率与该区间是开的还是闭的无关。注意概率P{x=a}=0,但{x=a}不是不可能的事件。
由于随机变量X的值只取决于概率密度函数的积分,所以概率密度函数在单个点上的值并不影响随机变量的性能。
如果一个函数和概率密度函数X只有有限数量的不同的值,可数无限或对整个实数线,这项措施是零(0组测量),然后函数也可以X的概率密度函数。
参考资料:百度百科——概率密度函数
概率论 二维期望的求法
没问题可以的,可以这样理解
二维随机变量求Eg(X,Y)=∬g(x,y)f(x,y)dxdy
你说的EX就相当于g(X,Y)=X的情况,这时EX=∬xf(x,y)dxdy。
二维条件数学期望怎么求
二维随机变量求Eg(X,Y)=∬g(x,y)f(x,y)dxdy 你说的EX就相当于g(X,Y)=X的情况,这时EX=∬xf(x,y)dxdy。