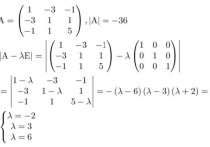系数矩阵的通解怎么求 由系数矩阵如何得出通解?如图怎么算的?
求解矩阵方程和通解,由系数矩阵如何得出通解?如图怎么算的?已知系数矩阵和特解,求通解,这个系数矩阵是怎么算出来的?系数矩阵如图所示 求基础解系,线性代数,这题通解怎么得来的?
本文导航
求解矩阵方程和通解
c
易见,A可以逆
则,X=A逆*B
第二题
把系数矩阵的增广阵写出来,再初等变形
2 1 -1 1 1
3 -2 1 -3 4
1 4 -3 5 -2
得
1 0 -1/7 -1/7 6/7
0 1 -5/7 9/7 -5/7
0 0 0 0 0
则,令x3和x4为自由向量
得通解=c(1/7 5/7 1 0)转置 加 d(1/7 -9/7 0 1)转置 加 (6/7 -5/7 0 0)转置
其中c and d为任意实数
你要记得,在这个式子里,凡是7的倍数都可以乘进去,比如c(1/7 5/7 1 0)转置也等价于c(1 5 7 0)
由系数矩阵如何得出通解?如图怎么算的?
最后一个矩阵等价于方程组
x1+x2-x3+x4=0
x2=0
3x3+x4=0
令x3=k,x4=-3k,x1=4k
(x1,x2,x3,x4)^T=(4k,0,k,-3k)^T=k(4,0,1,-3)^T
已知系数矩阵和特解,求通解
求基础解系与通解,过程如下:
这个系数矩阵是怎么算出来的?
首先观察三个约束方程一共有5个变量,分别为x1,x2,s1,s2,s3,每个方程并非都显式写出了5个变量,那么对于每个方程把缺少的变量的补上去,得到如下方程组:
x1+x2+s1+0s2+0s3=300,
2x1+x2+0s1+s2+0s3=400,
0x1+x2+0s1+0s2+s3=250.
提取变量前的系数,得到如下系数矩阵,和图中给出的系数矩阵相同。
1; 1; 1; 0; 0
2; 1; 0; 1; 0
0; 1; 0; 0; 1
扩展资料:
对于线性方程组,分为齐次的和非齐次,以下给出两种线性方程组的解法。
1、对于齐次方程组,我们通常就是列出其系数行列式,一步一步化成行阶梯型,再化成行最简型。然后求解,一般基础解系里面解向量的个数等于未知数的个数减去系数行列式的秩。
2、对于非齐次方程组,我们的解法是通解加特解的方法,所谓通解,就是先解出非齐次方程组所对应其次方程组的基础解系,然后再随便找一个特解满足非齐次方程组即可,然后把它们相加组合起来,就是非齐次方程组的解。
参考资料来源:百度百科-系数矩阵
系数矩阵如图所示 求基础解系
r(A) =1 ,基础解系的解向量的个数为 3-1 =2
令x2=1,x3=0,得x1=-1,α1=(-1,1,0)T
令x2=0,x3=1,得x1=1,α2=(1,0,1)T
基础解系为,α1,α2
写出系数矩阵为
2 -1 1 -1
2 -1 0 -3
0 1 3 -6
2 -2 -2 5 r2-r1,r4-r1,r1+r3
~
2 0 4 -7
0 0 -1 -2
0 1 3 -6
0 -1 -3 6 r4+r3,r1+4r2,r3+3r2,r2*-1,交换r2r3
~
2 0 0 -15
0 1 0 -12
0 0 1 2
0 0 0 0
于是得到矩阵的解为c(15,24,-4,2)^T,c为常数。
扩展资料:
要证明一组向量为齐次线性方程组AX=0的基础解系时,必须满足:
(1)这组向量是该方程组的解;
(2)这组向量必须是线性无关组;
基础解系的解向量个数是确定的,但解向量是不确定的,只要两两之间线性无关即可。基础解系的任意线性组合构成了该齐次线性方程组AX=0的一般解,也称通解 。
参考资料来源:百度百科-基础解系
线性代数,这题通解怎么得来的?
就是求齐次线性方程组AX=O的通解。
首先将系数矩阵A进行初等行变换,化成行最简形,过程如图。
x1、x2是阶梯头,所以x3是自由未知量。令x3=k,就可以求出方程组的通解,最后表示成向量的形式即可。