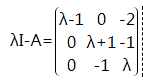矩阵特征多项式怎么写 matlab中怎么求矩阵特征多项式
矩阵的特征多项式怎么求?matlab中怎么求矩阵特征多项式?矩阵特征多项式的计算,特征多项式怎么求?矩阵的特征多项式怎么求?矩阵的特征多项式是什么?
本文导航
矩阵的特征多项式怎么求?
我告诉你吧。我最近发现了一个定理:n阶矩阵的特征多项式的n-i次方的系数为矩阵A的所有i阶主子式之和再乘以-1的i次方。我用M[i]表示A的所有i阶主子式之和。并规定M[0]=1;易知M[1]=tr(A);M[n]=|A|等;但这样算太麻烦我能通常是算特征值的你可以把|λE-A|的各行(或各列)加起来,若相等,则把相等的部分提出来(一次因式)后,剩下的部分是二次多项式,肯定可以分解因式。 2、把|λE-A|的某一行(或某一列)中不含λ的两个元素之一化为零,往往会出现公因子,提出来,剩下的又是一二次多项式
matlab中怎么求矩阵特征多项式
根据所知的矩阵,直接用poly生成特征多项式,或用eig命令求出特征值,再用poly生成多项式,。如:
a=magic(4);b=eig(a),d=poly(b),c=poly(a)
结果是:
b =
34.0000
8.9443
-8.9443
0.0000
d =
1.0e+03 *
0.0010 -0.0340 -0.0800 2.7200 -0.0000
c =
1.0e+03 *
0.0010 -0.0340 -0.0800 2.7200 -0.0000
c和d是一样的,也就是说,特征多项式就是:y=x^4-34*x^3-8*x^2+272*x
矩阵特征多项式的计算
特征矩阵如上,求其行列式,即特征多项式
按第1列展开,得到2阶行列式,然后按对角线法则展开,得到
(λ-1)[(λ+1)λ-1]
=(λ-1)(λ^2+λ-1)
=(λ-1)[(λ^2+λ+1)-2]
=(λ^3-1)-2(λ-1)
=λ^3-2λ+1
特征多项式怎么求?
解法:
1、把|λE-A|的各行(或各列)加起来,若相等,则把相等的部分提出来(一次因式)后,剩下的部分是二次多项式,肯定可以分解因式。
2、把|λE-A|的某一行(或某一列)中不含λ的两个元素之一化为零,往往会出现公因子,提出来,剩下的又是一二次多项式。
3、试根法分解因式。
扩展资料性质:
当A为上三角矩阵(或下三角矩阵)时,
;,其中;;是主对角线上的元素。对于二阶方阵,特征多项式能表为
;。一般而言,若;;,则
;。
此外:
(1)特征多项式在基变更下不变:若存在可逆方阵 C使得
;,则;;。
(2)对任意两方阵;;,有;;。一般而言,若A为;;矩阵,B 为;;矩阵(设;;),则;;。
(3)凯莱-哈密顿定理:
;。
参考资料:百度百科-特征多项式
矩阵的特征多项式怎么求
特征矩阵如上,求其行列式,即特征多项式。
按第1列展开,得到2阶行列式,然后按对角线法则展开,得到:
(λ-1)[(λ+1)λ-1]
=(λ-1)(λ^2+λ-1)
=(λ-1)[(λ^2+λ+1)-2]
=(λ^3-1)-2(λ-1)
=λ^3-2λ+1
对于求解线性递推数列,我们还经常使用生成函数法,而对于常系数线性递推数列,其生成函数是一个有理分式,其分母即特征多项式。
为n*n的矩阵A的特征多项式为|A-λE|,其中E为n*n的单位矩阵。
扩展资料:
特征多项式解法:
1、把|λE-A|的各行(或各列)加起来,若相等,则把相等的部分提出来(一次因式)后,剩下的部分是二次多项式,肯定可以分解因式。
2、把|λE-A|的某一行(或某一列)中不含λ的两个元素之一化为零,往往会出现公因子,提出来,剩下的又是一二次多项式。
3、试根法分解因式。
对布于任何交换环上的方阵都能定义特征多项式。要理解特征多项式,首先需要了解一下特征值与特征向量,这些都是联系在一起的:
设A是n阶矩阵,如果数λ和n维非零列向量x使得关系式Ax=λx成立,那么,这样的数λ就称为方阵A的特征值,非零向量x称为A对应于特征值λ的特征向量。
参考资料来源:百度百科——特征多项式
矩阵的特征多项式是什么
|a-
λe|=0是矩阵a的特征方程,|a-
λe|就是矩阵a的特征多项式啊,你要问什么,请说清楚,是求特征值或特征向量吗?