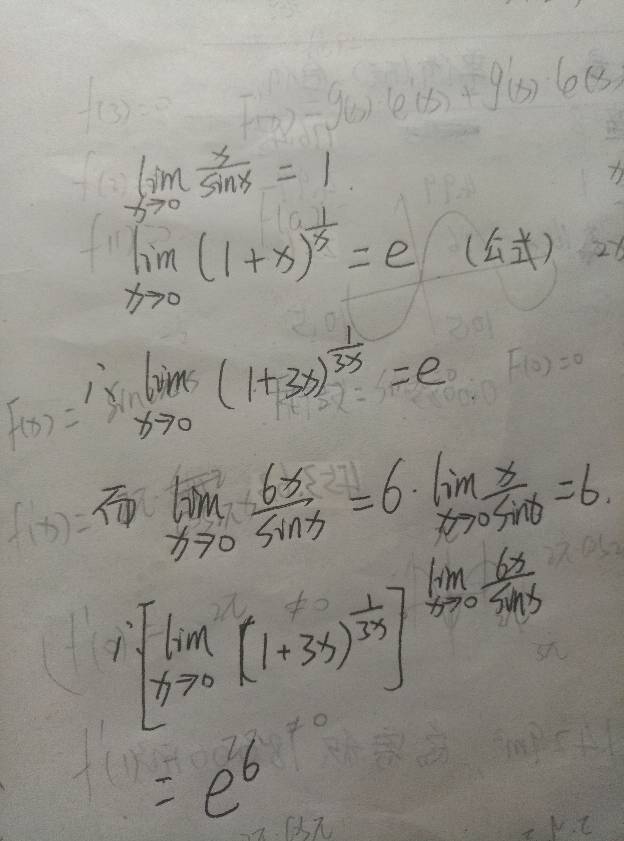为什么对指数求极限 求极限常见的六种方法
求指数函数的极限为什么是只要求指数的极限就行了?有点不是太懂!请详细的讲一下!我是高职的学生?为什么可以直接对幂的指数求极限?求大神证明?求大神证明为什么指数也能求极限?也看过一些解释,看不懂。。?为什么指数函数ex求极限时要分侧讨论?指数函数的极限,为什么这个求解极限的题中,可以将指数部分单独拿下来求极限?
本文导航
对数跟指数的极限怎么求
这个要用数学符号来表述,有点难度,这里插不进来符号。只好这样简单的说下了,指数趋于一个值。那么整个幂的值就趋于一个值,因为,指数函数是一一对应的
关于幂的运算的三个公式
这个用复合函数的连续性可以证明,u^v=e^vlnu得到幂指函数的等价式,由复合函数的连续性可知等式成立。
带X的式子都要求极限
求极限常见的六种方法
见图
指数函数极限公式
答:这是所有分式函数的特点,在t→0的条件下,奇函数1/t(可以把x-C看作是t)一定会有2个答案;这是做题中特别要注意的问题,遇到这样的问题,都需要分侧讨论。由于受(1/x)的影响,指数函数遇到这种情况,也都要进行分侧讨论。只有当f(x)是偶函数的情况下,不用分侧讨论。
只要多做题,每个人都会懂得何时要分侧讨论,何时不必分侧讨论。
指数函数的运算法则证明
以e为底指数函数求极限。
想一下指数函数的图像,x→-∞时为0,x→+∞时为无穷大,x→0-时1/x是-∞,e^1/x→0,直接用0替换就行了,x→0时1/x时是+∞,e^1/x→+∞,正无穷大没法直接带。
a>1时,则指数函数单调递增;若0单调递减的。
可以看到一个显然的规律,就是当a从0趋向于无穷大的过程中(不等于0)函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置,趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。其中水平直线y=1是从递减到递增的一个过渡位置。
基本性质在函数中可以看到:
(1) 指数函数的定义域为R,这里的前提是a大于0且不等于1。对于a不大于0的情况,则必然使得函数的定义域不连续,因此我们不予考虑,同时a等于0函数无意义一般也不考虑。
(2) 指数函数的值域为(0, +∞)。
(3) 函数图形都是上凹的。
求极限的例题及答案
用洛必达法则
这属于0/0型,对分子分母分别求导后,再算极限