函数极限左右极限是什么 求函数的极限方法
什么是左极限右极限?函数得左右极限怎么理解。可否讲解后举一个例子?极限的左右极限具体怎么求啊,不是直接带数吗?不是很理解…?怎样分别求函数的左极限和右极限?函数f(x)=X/X 的左右极限分别是什么?当x趋向于零的时候极限是否存在?怎么求函数的左右极限?
本文导航
左极限和右极限例题
左极限就是函数从一个点的左侧无限靠近该点时所取到的极限值,且误差可以小到我们任意指定的程度,只需要变量从坐标充分靠近于该点。
右极限就是函数从一个点的右侧无限靠近该点时所取到的极限值,且误差可以小到我们任意指定的程度,只需要变量从坐标充分靠近于该点。
左极限与右极限统称单侧极限。
扩展资料:
极限的来源:
与一切科学的思想方法一样,极限思想也是社会实践的大脑抽象思维的产物。极限的思想可以追溯到古代,例如,祖国刘徽的割圆术就是建立在直观图形研究的基础上的一种原始的可靠的“不断靠近”的极限思想的应用。
古希腊人的穷竭法也蕴含了极限思想,但由于希腊人“对’无限‘的恐惧”,他们避免明显地人为“取极限”,而是借助于间接证法——归谬法来完成了有关的证明。
到了16世纪,荷兰数学家斯泰文在考察三角形重心的过程中,改进了古希腊人的穷竭法,他借助几何直观,大胆地运用极限思想思考问题,放弃了归缪法的证明。如此,他就在无意中“指出了把极限方法发展成为一个实用概念的方向”。
参考资料:百度百科---左极限
参考资料:百度百科---右极限
函数求极限方法归纳
函数的左极限:从一个地方(比如坐标轴)的左侧无限趋向于常数a所取的极限值(x→a-),或者从0无限趋向于这个地方的左侧所取的极限值(x→∞-),则称为函数的左极限。
函数的右极限:从一个地方(比如坐标轴)的右侧无限趋向于常数a所取的极限值(x→a+),或者从0无限趋向于这个地方的右侧所取的极限值(x→∞+),则称为函数的右极限。
如e^(1/x),判断它在x→0时是否存在极限。
当x→0-时,lim[x→0-]e^(1/x)=0;
当x→0+时,lim[x→0+]e^(1/x)=∞;
此函数左右极限不相等,所以它关于x→0的极限不存在。
扩展资料:
左极限与右极限只要有其中有一个极限不存在,则函数在该点极限不存在。常用的函数极限的性质有函数极限的唯一性、局部有界性、保序性以及函数极限的运算法则和复合函数的极限等等。
在运用以上两条去求函数的极限时尤需注意以下关键之点。
一是先要用单调有界定理证明收敛,然后再求极限值。
二是应用夹挤定理的关键是找到极限值相同的函数 ,并且要满足极限是趋于同一方向 ,从而证明或求得函数的极限值。
洛必达法则是分式求极限的一种很好的方法,当遇到分式0/0或者∞/∞时可以采用洛必达,其他形式也可以通过变换成此形式。
洛必达法则:符合形式的分式的极限等于分式的分子分母同时求导。
参考资料来源:百度百科——右极限
参考资料来源:百度百科——左极限
极限中几个常用公式
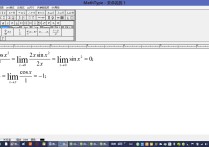
极限的左右极限不能直接带入,这两道题应该根据洛必达法则来求。
这两道题的极限都不能直接将x带入,因为所求极限的函数的取值范围中都没有0。xlnx的取值范围为(x>0),(1/x)lnx的取值范围为(x大于0),所以不能直接带入x=0来求。
第一道:x趋近于0是limxlnx可写成limlnx/(1/1/x),根据洛必达法则,limlnx/(1/1/x)=lim(1/x)/(-1/x的平方),约分可得lim(-x),x趋近于0时lim(-x)=0,即x趋近于0时limxlnx=0。
第二道:x趋近于0时lim(1/x)lnx根据洛必达法则,等于lim(1/x),x趋近于0时lim(1/x)趋近于∞,即x趋近于0时,lim(1/x)lnx趋近于∞。
扩展资料:
在运用洛必达法则之前,首先要完成两项任务:
一是分子分母的极限是否都等于零(或者无穷大);
二是分子分母在限定的区域内是否分别可导。
如果这两个条件都满足,接着求导并判断求导之后的极限是否存在:如果存在,直接得到答案;如果不存在,则说明此种未定式不可用洛必达法则来解决;如果不确定,即结果仍然为未定式,再在验证的基础上继续使用洛必达法则。
洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。 众所周知,两个无穷小之比或两个无穷大之比的极限可能存在,也可能不存在。
因此,求这类极限时往往需要适当的变形,转化成可利用极限运算法则或重要极限的形式进行计算。洛必达法则便是应用于这类极限计算的通用方法。
参考资料来源:百度百科-洛必达法则
求函数的极限方法
函数的左极限从一个点的左侧无限靠近该点时所取到的极限值,且误差可以小到任意指定的程度,只需要变量从坐标充分靠近于该点。
函数的右极限从一个点的右侧无限靠近该点时所取到的极限值,且误差可以小到我们任意指定的程度,只需要变量从坐标充分靠近于该点。
扩展资料:
左极限与右极限统称单侧极限。
函数f(x),当x——>x^0时,极限存在,当且仅当函数f(x)在x——>x^0处左极限和右极限都存在,且两者相等。用数学表达式表示为:
存在
和
都存在且
函数fx在x=x0处取极大值的条件
1、函数f(x)=X/X 的左右极限都是1,当x趋向于零的时候极限存在,且等于1;
2、函数极限是高等数学最基本的概念之一,导数等概念都是在函数极限的定义上完成的;
3、函数极限性质的合理运用。常用的函数极限的性质有函数极限的唯一性、局部有界性、保序性以及函数极限的运算法则和复合函数的极限。
扩展资料:
函数极限介绍:
以
的极限为例,f(x) 在点
以A为极限的定义是: 对于任意给定的正数ε(无论它多么小),总存在正数
,使得当x满足不等式
时,对应的函数值f(x)都满足不等式:
,那么常数A就叫做函数f(x)当 x→x。时的极限。
参考资料来源:百度百科-函数极限
求函数极限的各步骤怎么写
x→0-,就是x从0的左侧趋向于0,所以x<0,如果x→0+,就是x从0的右侧趋向于0,x0.同理x→1-,就是x从1的左侧趋向于1,所以x<1,如果x→1+,就是x从1的右侧趋向于1,x1.例如:lim[x→1-]
f(x)
注意此时x<1
=lim[x→1-]
(x-1)=0
lim[x→1+]
f(x)
此时x1
=lim[x→1+]
(2-x)=1
左右极限不等,因此函数在x=1处为跳跃间断点
x-1和2-x都是初等函数,这种初等函数求极限时只要能直接算函数值就,就代值直接算就行