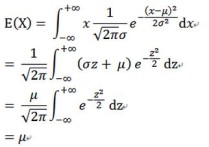分段函数怎么求极限 分段函数极限怎么算

分段函数的极限如何求？分段函数极限怎么算？分段函数求极限，分段函数求极限，关于分段函数极限。

本文导航

• 分段函数的极限如何求
• 分段函数极限怎么算
• 分段函数求极限？
• 分段函数求极限
• 关于分段函数极限

分段函数的极限如何求

那要看求函数什么点处的极限.

如果求函数在间断点处的极限，则需求函数在间断点处的左、右极限，（左、右极限是两个不同解析式的极限）只有当函数的左、右极限都存在且相等时，函数的极限才存在，否则函数极限不存在；

如果求函数在非间断点（连续点）处的极限，那就简单多了，只需求临近点处函数的极限即可.

不知道我说明白没有，有疑问可追问，祝你学习进步！

分段函数极限怎么算

主要是在分段处考察，内容：1、在分段处是否有定义，定义是否连续，如果连续左右极限必然相等；2、如果没有定义，考察函数的左右极限是否相等，如果相等，为可去间断点，否则，为不可去间断点。

例如间断点为x=a，左极限为lim(△x→0) [f(a-0+△x)-f(a-0)]/△x,用左端的函数计算；

右极限为lim(△x→0) [f(a+0+△x)-f(a+0)]/△x 用a点右边的函数计算。

分段函数求极限？

x=1时，

f（1）=[2的n分之一次方/2]×sin兀

=0。

你的认为是正确的！

它确实也是这么计算岀来的，

你们是一致的，并没有什么矛盾呀？

你为啥子还有疑惑了呢？！

你再冷了静的看看它的解答，

想想看看，的确一致呀。

分段函数求极限

①存在

②不存在

③=0

方法如下，请作参考：

关于分段函数极限

按照x>0时的函数表达式去计算x→0+的极限，如果极限存在，则表明x=0处右极限存在。如果x→0-时的左极限也存在，且二者相等，则可以说函数在x=0处极限存在。

求函数值域：

求函数f(x)= 的值域。

解：当-2≤x≤a时，x2 的取值有三种情形：

（1）当-2≤a<0时,有a2≤x2≤4 。

(2)当0≤a≤2时,有0≤x2≤4 。

(3)当a>2时,有0≤x2≤a2。

当x>a时，-|x|的取值有两种情形：

（1）当-2≤a<0时，有-|x|≤0。

（2）当a≥0时，有－|x|<-a 。

所以原函数的值域为：

（1）当-2≤a<0时,为(-∞,0]∪[a2,4] 。

（2）当0≤a≤2时,为(-∞,-a)∪[0,4]。

（3）当a>2时,为(-∞,-a)∪[0,a2]。

求分段函数的值域的方法：分别求出各段函数在其定义区间的值域，再取它们的并集即可。