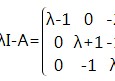矩阵特征值怎么理解 如何理解矩阵特征值
如何理解矩阵特征值?如何理解矩阵特征值?如何理解矩阵特征值?
本文导航
如何理解矩阵特征值
首先需要了解的是方阵A的特征值的求法:f(λ)=|λE-A|=0的根。
矩阵的特征值与其对应的特征向量还有矩阵的不变因子都是属于矩阵的一个不变量,是我们了解矩阵的一个重要结果。建议你查看一下高等代数λ—矩阵不变因子章节。
矩阵的特征值是对应的Aξ=λξ(ξ为λ对应下的特征向量),这有点类似于函数不动点的性质(使得g(x)=x的x称为其不动点)
如何理解矩阵特征值
1.定义:若矩阵A乘上某个非零向量α等于一个实数λ乘上该向量,即Aα=λα,则称λ为该矩阵的特征值,α为属于特征值λ的一个特征向量。
2.求矩阵A的特征值及特征向量的步骤:
(1)写出行列式|λE-A|;
(2)|λE-A|求=0的全部根,它们就是A的全部特征值,其中E为单位矩阵;
(3)对于矩阵A的每一个特征值λ,求出齐次线性方程组(λE-A)X=0的一个基础解系,则可以得到属于特征值λ的特征向量。
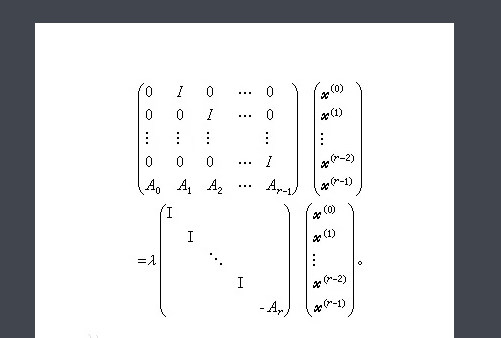
3.特征值的作用和意义体现在用矩阵进行列向量的高次变换也就是矩阵的高次方乘以列向量的计算中。数学中的很多变换可以用矩阵的乘法来表示,在这样的变换中,一个列向量(点)α变成另一个列向量(点)β的过程可以看成是一个矩阵A乘以α得到β,即Aα=β,如果把同样的变换连续的重复的做n次则需要用矩阵高次方来计算:A^n·α,如果没有特征值和特征向量,此处就要计算矩阵A的n次方,这个运算量随着n的增加,变得越来越大,很不方便。而利用特征值和特征向量,可以达到简化计算的目的:设A特征值分别为λ1,λ2,------λk,对应的特征向量分别为α1,α2,------αk,且α可以分解为α=x1·α1+x2·α2+---+xk·αk,
则A^n·α=A^n·(x1·α1+x2·α2+---+xk·αk)
=A^n·x1·α1+A^n·x2·α2+---+A^n·xk·αk
=x1A^n·α1+x2A^n·α2+---+xkA^n·αk
=x1(λ1)^n·α1+x2(λ2)^n·α2+---+xk(λk)^n·αk.
这样就将矩阵的n次方的运算变成了特征值的n次方的运算。
矩阵特征值的个数怎么求
如下:
设 A 是n阶方阵,如果存在数m和非零n维列向量;x,使得 Ax=mx 成立,则称 m 是矩阵A的一个特征值(characteristic value)或本征值(eigenvalue)。
矩阵特征值性质:
性质1:若λ是可逆阵A的一个特征根,x为对应的特征向量,则1/λ 是A的逆的一个特征根,x仍为对应的特征向量。
性质2:若 λ是方阵A的一个特征根,x为对应的特征向量,则λ 的m次方是A的m次方的一个特征根,x仍为对应的特征向量。