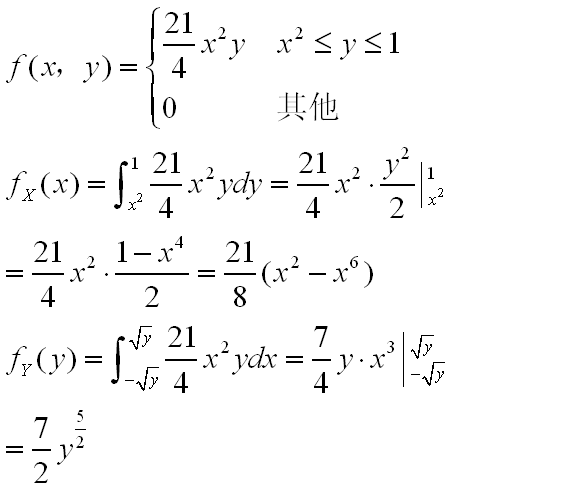边缘密度概率怎么求 概率论,求边缘概率密度函数。在线等
概率论 图中的边缘概率密度如何得出??概率论,求边缘概率密度,最好给出详细过程,求边缘概率密度函数,概率论,求边缘概率密度函数。在线等,已知概率密度函数,求边缘概率密度函数,如何求y的边缘概率密度?
本文导航
概率论 图中的边缘概率密度如何得出?!
分别对y和x在定义域内求积分即可,比如y从x²到1对联合密度积分
概率论的求解方法
概率论是研究随机性或不确定性等现象的数学。更精确地说,概率论是用来模拟实验在同一环境下会产生不同结果的情况。存在大量的随机现象,而概率是衡量该现象发生的可能性的量度。
随机现象的实现和对它的观察称为随机试验。在一次随机试验中发生某个事件是带有偶然性的,但那些可以在相同条件下大量重复的随机试验却往往呈现出明显的数量规律性,人们在长期实践中已逐步觉察到某些这样的规律性,并在实际中应用它,这便形成了概率论。
现代概率论的主要分支有概率空间、随机变量与概率分布、数字特征与特征函数、随机极限理论、金融数学等。
随着人类的社会实践,人们需要了解各种不确定现象中隐含的必然规律性,并用数学方法研究各种结果出现的可能性大小,从而产生了概率论,并使之逐步发展成一门严谨的学科。概率与统计的方法日益渗透到各个领域,并广泛应用于自然科学金融保险甚至人文科学中。
一个随机试验所包含的单位事件是有限的,且每个单位事件发生的可能性均相等,则这个随机试验叫做拉普拉斯试验
求边缘概率密度函数
根据变量的范围,对联合概率密度函数进行积分,得到Y积分的边际概率密度,得到X积分的边际概率密度如下:
扩展资料:
连续型随机变量的概率密度函数有如下性质:
如果概率密度函数fX(x)在一点x上连续,那么累积分布函数可导,并且它的导数:
由于随机变量X的取值 只取决于概率密度函数的积分,所以概率密度函数在个别点上的取值并不会影响随机变量的表现。
更准确来说,如果一个函数和X的概率密度函数取值不同的点只有有限个、可数无限个或者相对于整个实数轴来说测度为0(是一个零测集),那么这个函数也可以是X的概率密度函数。
连续型的随机变量取值在任意一点的概率都是0。作为推论,连续型随机变量在区间上取值的概率与这个区间是开区间还是闭区间无关。要注意的是,概率P{x=a}=0,但{X=a}并不是不可能事件。
概率论,求边缘概率密度函数。在线等
边缘概率密度函数 ∫『-∞,+∞』3y/2 dx 0<y<1fy(y) = 0 其他即 ∫『-y,y』3y/2 dx 0<y<1fy(y) = 0 其他即 3y² 0<y<1fy(y) = 0 其他
已知概率密度函数,求边缘概率密度函数
根据变量的取值范围,对联合概率密度函数积分,对y积分得到X的边缘概率密度,对x积分得到Y的边缘概率密度过程如下:
扩展资料:
由于随机变量X的取值 只取决于概率密度函数的积分,所以概率密度函数在个别点上的取值并不会影响随机变量的表现。更准确来说,如果一个函数和X的概率密度函数取值不同的点只有有限个、可数无限个或者相对于整个实数轴来说测度为0(是一个零测集),那么这个函数也可以是X的概率密度函数。
连续型的随机变量取值在任意一点的概率都是0。作为推论,连续型随机变量在区间上取值的概率与这个区间是开区间还是闭区间无关。要注意的是,概率P{x=a}=0,但{X=a}并不是不可能事件。
最简单的概率密度函数是均匀分布的密度函数。
对于一个取值在区间[a,b]上的均匀分布函数;;,它的概率密度函数:;也就是说,当x不在区间[a,b]上的时候,函数值等于0;而在区间[a,b]上的时候,函数值等于这个函数;;。这个函数并不是完全的连续函数,但是是可积函数。
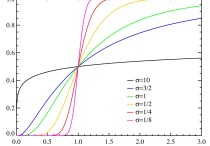
正态分布是重要的概率分布。它的概率密度函数是:
随着参数μ和σ变化,概率分布也产生变化。
如何求y的边缘概率密度
y的边缘密度函数 (0,(y-1)/2)的积分范围对x积分
x的边缘密度函数 (0,2x+1)的积分范围对y积分
积分范围首先要画出积分区域,如果要求x的边缘密度,那就首先固定x,也就是画一条竖线,然后看y的范围